عملکرد متالورژیکی تاندیش در ریخته گری مداوم

مطالعات محاسباتی سیستم عملکرد متالورژیکی تاندیش فولادسازی به اوایل دهه هشتاد باز می گردد. دو مطالعه کلی جداگانه به ترتیب در سال های 1999 و 2010 منتشر شده که در آن ها مطالعات بسیاری که توسط محققین زیادی صورت گرفته را خلاصه نموده است. این مطالعات نشان می دهد که مدلسازی عملکرد متالورژیکی تاندیش ابتدائا به حالت فرآیندی پایا محدود می شد و پدیده هایی چون: جریان سیال، توربولانس، اختلاط مواد و حرارت، شناوری ناخالصی ها و حذف بسیار مورد توجه قرار گرفتند. در این راستا، مدلسازی جریان های هموژن و آشفته نسبتا رایج تر است. از سال 2008 یا پس از آن، مدلسازی گذرا و چندفازی متالورژی سیستم تاندیش مورد توجه و محبوب واقع شده و گزارشاتی از برخی محققین در این زمینه منتشر شده است. این مقاله خلاصه ای کوتاه و ارزیابی انتقادی از این تلاش ها را در مقابل عملکرد متالورژیکی تاندیش در صنعت ارائه می دهد. علی رغم پیشرفت ها در تئوری و روش های محاسباتی، پیشرفت در مدلسازی عملکرد متالورژیکی تاندیش (خصوصا در دهه گذشته) تا حدودی کند بوده است. در بخش نهایی این مقاله، گزارشی از تلاش های مستمر نویسنده و همکارانش ارائه شده که در آن مدلسازی جریان دوفازی در لدل شرود و اثرات آن بر عملکرد متالورژیکی تاندیش فولادسازی مورد بحث قرار می گیرد.

مقدمه:

از زمان معرفی ریخته گری مداوم در دهه هفتاد، متالورژی پاتیل و عملکرد متالورژیکی تاندیش اهمیت قابل توجهی یافت و بر این اساس، نوآوری های بسیاری به طور سیستماتیک در عرصه فولادسازی تجاری معرفی شد. در فرآیند ریخته گری مداوم انتقال فولاد مذاب از پاتیل به قالب به واسطه عملکرد متالورژیکی تاندیش صورت می گیرد که با معرفی اسلایدگیت، لدل شرود، اصلاح‌ساز جریان، دمش گاز از طریق استوپر و… این فرآیند تغییرات قابل توجهی داشته است. در فرآیند ریخته گری مداوم انتقال فولاد مذاب از پاتیل به قالب به واسطه عملکرد متالورژیکی تاندیش صورت می گیرد که با معرفی اسلایدگیت، لدل‌شرود، اصلاح‌ساز جریان، دمش گاز از طریق استوپر و … این فرآیند تغییرات قابل توجهی داشته است. این موارد تا حد زیادی مانع افت کیفیت فولاد شدند و قابلیت ریخته گری بهتر و تمیزی محصول را که برای حفظ ریخته گری مداوم (به ویژه در بازه های طولانی) ضروری است تضمین نمودند. با توجه به پیشرفت‌های مختلف صنعتی و تقاضای روزافزون برای محصولات فولادی کیفیت بالا، فعالیت‌های تحقیقاتی قابل توجهی در زمینه عملکرد متالورژیکی تاندیش در دانشگاه و صنعت در طول دهه هشتاد دنبال شد و هنوز هم ادامه دارد. به طور کلی مدلسازی فیزیکی و ریاضیاتی به کارگرفته شد (در مواقعی این مدل ها با داده های به دست آمده از آزمایشات در مقیاس کارخانه تامین می شود) و پدیده های متفاوت مورد بررسی قرار گرفتند. به طور کلی مدلسازی فیزیکی و ریاضیاتی که در مواقعی با داده های به دست آمده از آزمایشات در مقیاس کارخانه تامین می شود به کارگرفته شد و پدیده های متفاوت مورد بررسی قرار گرفتند. این موارد موضوع مطالعات بسیار زیادی در منابع قرار گرفتند. خلاصه ای از کارهای تحقیقاتی صورت گرفته در بازه زمانی 1985 تا 2009 در دو رفرنس در سال های 1999 و 2010 منتشر شده است.

این دو رفرنس نشان می دهند که در سال های 1985 تا 2008 عمدتا مدل جریان های آشفته و هموژن به کار گرفته شده و عموما تمرکز بر مدلسازی پدیده هایی چون: توزیع زمان ماندگاری، شناوری ناخالصی ها و حذف، اتلاف حرارت و غیره در حین عملکرد پایدار سیستم تاندیش است. به طور موازی تلاش‌های چشمگیری برای مدل‌سازی پدیده آشفتگی در زمینه عملکرد متالورژیکی تاندیش انجام شد و در این زمینه‌، دستورالعمل‌های لازم اغلب از اندازه‌گیری‌های انجام‌شده در رابطه با عملکرد متالورژیکی تاندیش مدل آب استخراج می‌شد. نرم‌افزارهای قدرتمند دینامیک سیالات محاسباتی (CFD) در ارتباط با روش‌های محاسبه جریان چند فازی و منطق فیزیکی، نیروی محرکه لازم را فراهم نمود و از سال 2008 منجر به چندین مطالعه مدل‌سازی جریان دو و سه فازی شد. این مدل ها تا حد زیادی به محاسبه جریان گاز-مایع تحت شرایط جریان پایا، همدما و آشفته محدود می‌شدند. ابتدائا روش های محاسبه VOF (حجم سیال) و همچنین روش های ترکیبی VOF+DPM (مدل سازی فاز گسسته) پیشرفته شدند. مدل‌سازی چند فازی، غیر همدما، جریان واکنش‌دهنده (یعنی واکنش‌های سرباره-فلز یا گاز-فلز) عملیات سیستم تاندیش به ندرت یافته شده و مدل‌سازی جامع عملکرد متالورژیکی تاندیش تاکنون انجام نشده است. به طور مشابه، مدل‌سازی دو فازی و سه فازی عملیات‌های حالت ناپایا (مثلاً عملیات تعویض پاتیل یا شروع به کار) کمتر دقیق و نسبتاً کمیاب بوده است. در‌واقع، علی‌رغم پیشرفت‌های اصولی بسیار در تئوری ها، روش‌های عددی و نرم‌افزارهای توانمند CFD، پیشرفت در مدل‌سازی عملکرد متالورژیکی تاندیش،از سال 2000، تا حدودی کند بوده است. در نتیجه، تعداد و تکرار انتشارات آرشیوی در طول یک دهه گذشته به طور قابل توجهی کاهش یافته است. هدف کار فعلی ارائه مروری بر پیشرفت های مدلسازی سیستم تاندیش بعد از سال 2008 است آنالیزی منسجم از پیشرفت های مختلف در این زمینه ارائه می نماید.

در بخش‌های بعدی، ابتدا شرح مختصری از عملکرد متالورژیکی تاندیش و مدل‌سازی ریاضی آن‌ها ارائه می‌شود. سپس مروری بر آنالیز مطالعات مدل سازی جریان های چند فازی مختلف ارائه می شود. در بخش پایانی، شبیه‌سازی عددی دو عملیات متالورژی مختلف سیستم تاندیش ارائه می‌شود که اهمیت ادغام ویژگی‌های فرآیند واقعی و اندازه‌گیری‌ ها جهت ساپورت روش در مطالعات مدل ریاضی را برجسته می‌کند.

2. عملکرد متالورژیکی تاندیش و مدلسازی ریاضی

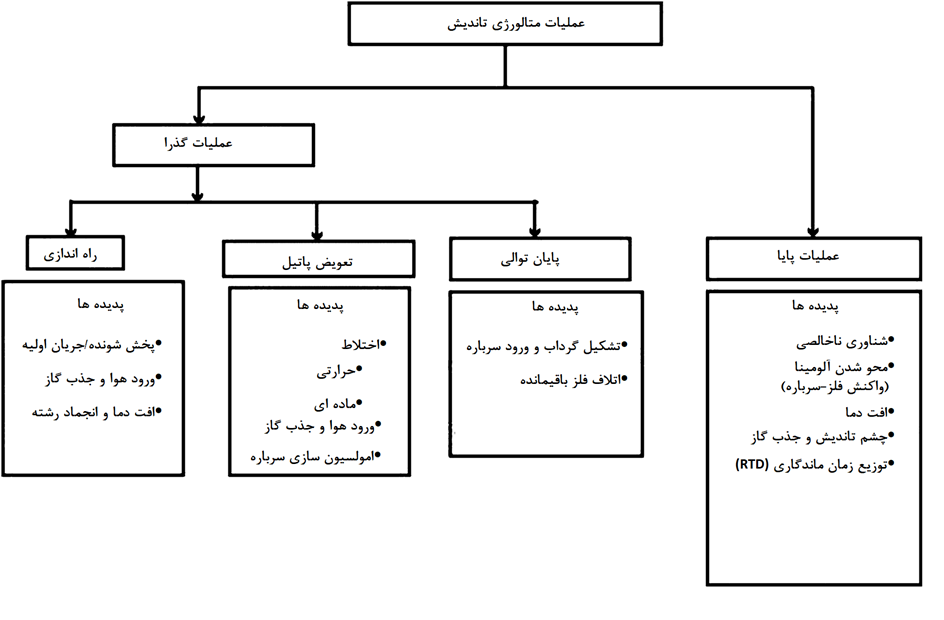
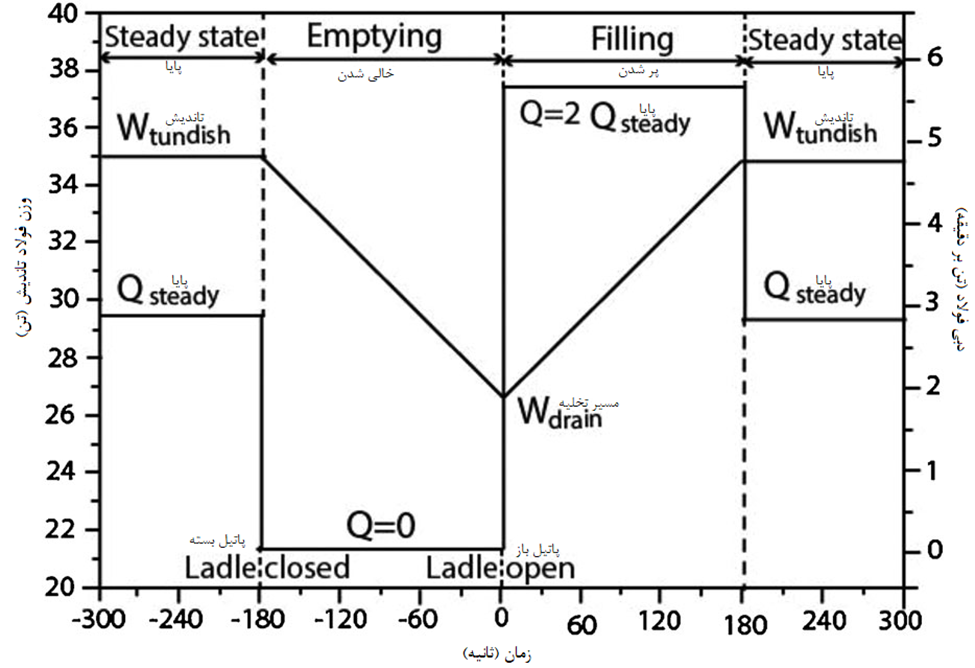
تاندیش یک عملگر واسط است که در آن فولاد مذاب معمولاً از یک ورودی وارد می شود و از یک یا چند خروجی خارج می شود. بجز هنگام پرکردن اولیه، تعویض پاتیل و مواقع تخلیه نهایی، عملکرد متالورژیکی تاندیش عملاً تحت شرایط حالت پایا کار می‌کند. بسته به اندازه و طول توالی، دوره های انتقالی می توانند اندک یا کسری قابل ملاحظه از مدت زمان حالت پایا باشند. پدیده های مختلف در دو دوره مشخصه مربوط به فولادسازان در شکل 1 خلاصه شده است.

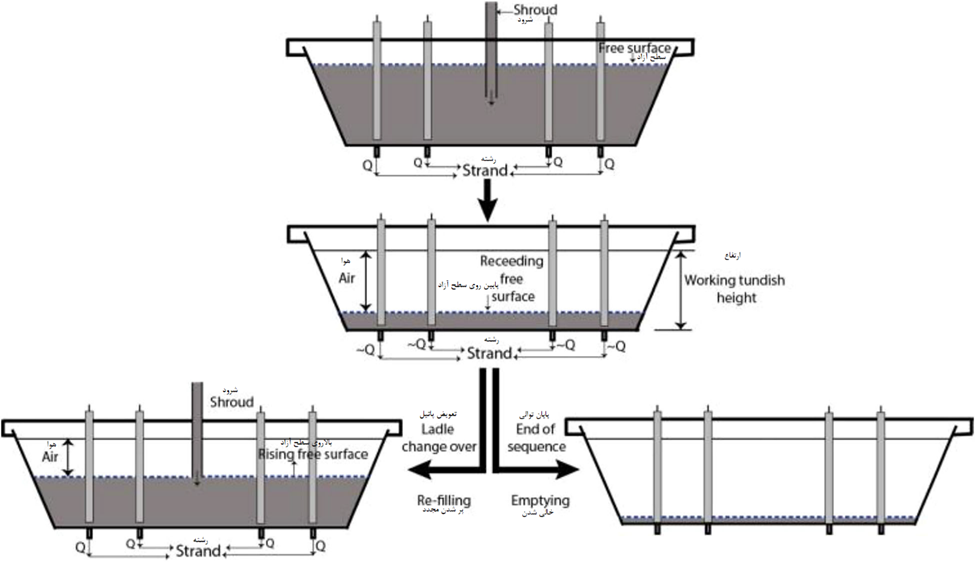
در طول راه اندازی، یک سیستم تاندیش پیشگرم شده (تقریبا در دمای 1250 درجه سانتیگراد یا بیشتر) برای انتقال ملایم و مداوم فولاد مذاب از یک پاتیل به یک قالب استفاده می شود. در ابتدا، مذاب از پاتیل با نرخی بیشتر از توان دبی عبوری یک سیستم تاندیش تغذیه می‌شود، به طوری که غوطه‌ور شدن سریع لدل شرود تضمین می‌شود تا اختلاط گاز-مایع-سرباره و جذب گاز در سیستم تاندیش به حداقل برسد. در چنین شرایطی، میله‌های استوپر به طور کامل پایین می‌مانند تا نازل‌های سیستم تاندیش را ببندند، به طوری که قبل از شروع ریخته‌گری، سریعا مقدار مناسبی از مذاب در سیستم تاندیش انباشته می شود. هنگامی که مقدار آستانه ای از مذاب انباشته می شود، میله های استوپر به تدریج بالا می روند و اجازه می دهند فولاد مذاب در قالب جریان یابد. در مدت کوتاهی نرخ ریخته‌گری یا دبی خروجی مورد نظر تثبیت می‌شود و نرخ جریان ورودی برای ایجاد حجم ثابت مذاب (یا ارتفاع مذاب ثابت) در سیستم تاندیش عملیاتی می‌شود.

تغییرات رایج پارامترهای عملیاتی کلیدی در حین کارکرد در شکل 2a و همچنین مراحل مربوط به کارکرد سیستم تاندیش به صورت شماتیک در شکل 2b نشان داده شده است. در حین مدت پر شدن تدریجی یک سیستم تاندیش، عامل‌های تشکیل دهنده سرباره مناسب مدام اضافه می شود تا پوشش سرباره محافظی را تشکیل دهد که برای محدود کردن تلفات تشعشع و کمک به جذب ناخالصی ها لازم است. تغییرات رایج پارامترهای عملیاتی کلیدی در حین کارکرد در شکل 2a نشان داده شده است، همچنین مراحل مربوط به عملکرد متالورژیکی تاندیش به صورت شماتیک در شکل 2b نشان داده شده است. در حین مدت پر شدن تدریجی یک سیستم تاندیش، عامل های تشکیل دهنده سرباره مناسب مدام اضافه می شود تا پوشش سرباره محافظی را تشکیل دهد که برای محدود کردن تلفات تشعشع و کمک به جذب ناخالصی ها لازم است. تمام سیستم تاندیش های مدرن در حین کار از نظر فیزیکی پوشیده می‌شوند تا از راندمان حرارتی و شیمیایی بالا اطمینان حاصل شود (به عنوان مثال، حداقل اتلاف گرما، قابل صرف نظر و ناچیز شدن نفوذ هوا، و غیره).

ورود اولیه فولاد مذاب به سیستم تاندیش، پخش شدن آن بر روی سطح نسوز و انباشت تدریجی آن بسیار مهم است، به ویژه برای پدیده انجماد رشته در سیستم‌های تاندیش ریخته‌گری بلوم که نسبت سطح به حجم زیادی دارند (به بخش بعدی رجوع شود). در طول راه اندازی و تا لحظه ای که نوک شرود در فولاد مذاب غوطه ور شود، هم زدن شدید سرباره-فلز و گاز برای تأثیرگذاری بر عملکرد متالورژیکی تاندیش فولادسازی انجام می شود. در طی چنین فرآیندی، اکسیداسیون مجدد شدید (در غیاب دمش آرگون در سیستم تاندیش)، فرسایش مواد گانینگ سیستم تاندیش و کشش زودهنگام سرباره همگی می توانند کیفیت فولاد ساخته شده از طریق عملیات های مختلف بالادستی (مانند BOF، LRF، VD و غیره) را از بین ببرند.

پس از راه اندازی، هنگامی که مذاب به سطح کاری تعیین شده رسید، عملکرد متالورژیکی تاندیش در حالت پایا با پارامترهای عملیاتی اصلی مانند دبی ورودی، نرخ توان عبوری مجرا، حجم فولاد مذاب و غیره عملاً ثابت می مانند. فعل و انفعالات سرباره و فلز در طول دوره حالت پایا عموماً کمتر مشخص می شود مگر اینکه آرگون از طریق لدل شرود به داخل تاندیش وارد شود (به بخش بعدی رجوع شود). پدیده های مورد توجه در هنگام برقراری جریان پایا عبارتند از: شناوری ناخالصی ها، توزیع زمان ماندگاری (RTD)، افت دما، ایجاد حالت چشمی شکل تاندیش، و واکنش های سرباره-فلز (مثلاً کاهش سیلیس موجود در سرباره تاندیش توسط آلومینیوم محلول در مذاب).

پدیده‌ های انتقالی در حین تعویض پاتیل و همچنین هنگام پایان فرآیند در عملکرد متالورژیکی تاندیش ظاهر می‌شوند (رجوع به شکل 1). در این مدت، جریان ورودی برای مدتی متوقف می شود و عمق حمام کاهش می یابد. بنابراین هر چقدر که مواد از یک پاتیل جدید به سیستم تاندیش تغذیه می‌شوند، اختلاط شدید حرارت و مواد نیز در میان سرباره مذاب و محیط (هوا) رخ می دهد. کشش سرباره و اتلاف فلزات باقیمانده نیز در طول عملیات تغییر پاتیل و پایان زنجیره عملیات به مسائل مهم تبدیل می شوند. حالت‌های فیزیکی ایده‌آل یک سیستم تاندیش، در هنگام تعویض پاتیل و پایان زنجیره عملیات، به صورت شماتیک در شکل 3 نشان داده شده است.

مباحث قبلی به وضوح نشان می‌دهد که جریان چند فازی، گرما، انتقال جرم و همچنین واکنش‌های شیمیایی بین فازهای مختلف (مذاب-سرباره-دیرگداز و هوا) از ویژگی‌های عملکرد متالورژیکی تاندیش است. بنابراین، مدل‌سازی فرآیند دقیق، طبیعتاً دشوار است و اغلب به دلیل چندین پدیده عارضی همچون فرسایش مواد نسوز و گانینگ، گرفتگی نازل، و همچنین نوسانات و اختلالات فرآیند پیچیده می‌شود.

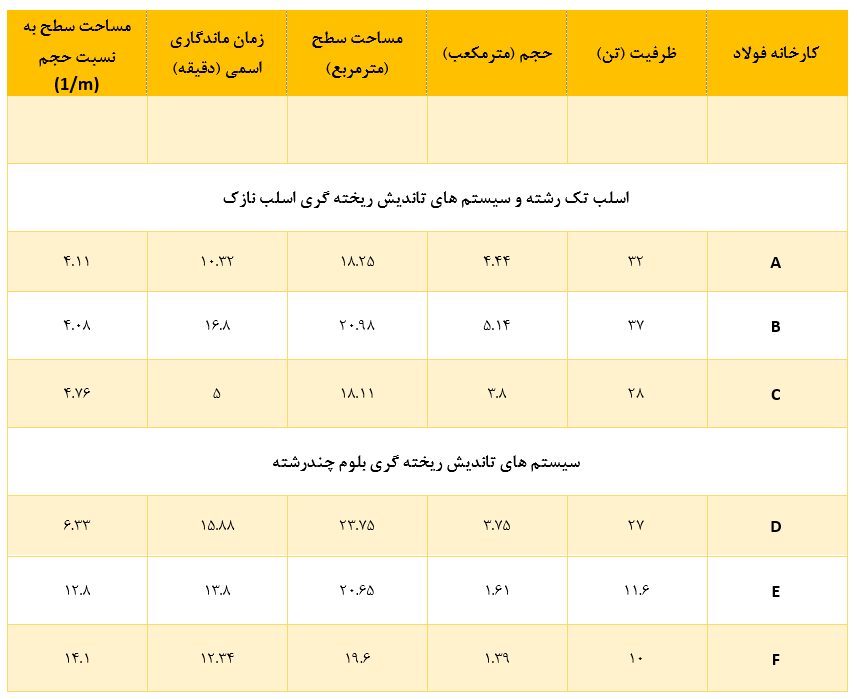
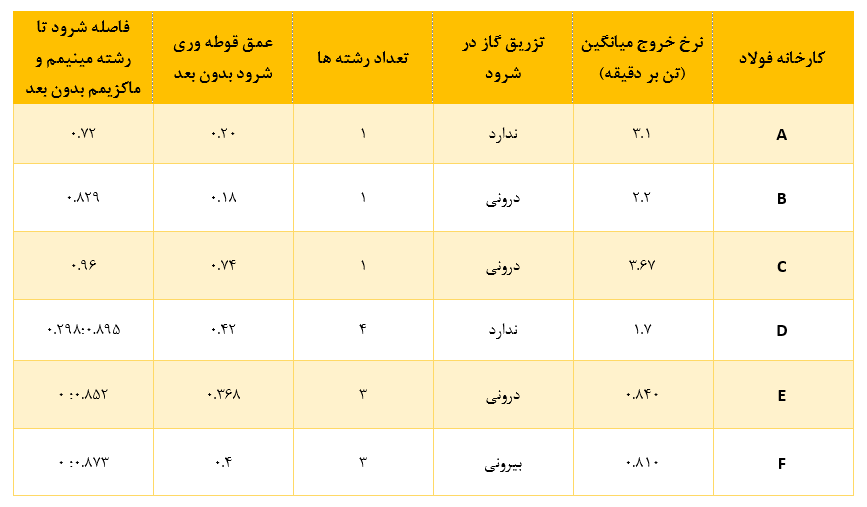
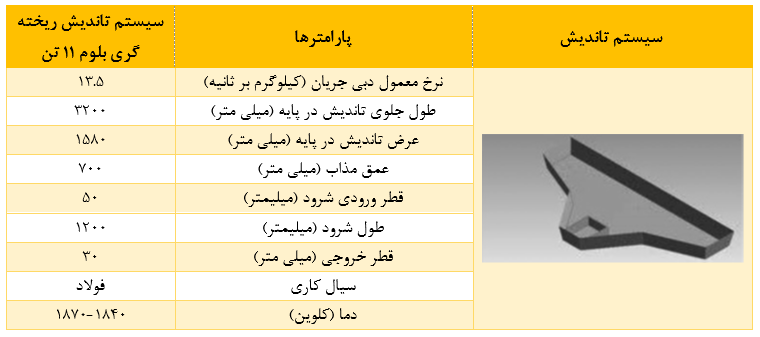
اشکال سیستم تاندیش، ظرفیت، ظرفیت دبی عبوری و پارامترهای عملیاتی در شش کارخانه فولاد، بازتولید شده از رفرنس [4]، به ترتیب در جدول 1 و 2 ارائه شده است. این پارامترها در هر کدام از کارخانه ها متفاوت است و بنابراین، زمان ماندگاری اسمی مربوط به هر کدام، نسبت سطح به حجم، عمق غوطه وری شرود، فاصله شرود تا رشته و سایر موارد در هر کارخانه نسبت به سایر کارخانه ها تا حد زیادی متفاوت است. در نتیجه عملکرد متالورژیکی سیستم‌های تاندیش فولادسازی در هر کارخانه منحصر به فرد و ویژگی مشخصه همان کارخانه است. بنابراین با این گستردگی اطلاعات راه‌حل‌های خاص برای بهبود عملکرد متالورژیکی تاندیش از طریق مدل‌سازی ریاضی پیچیده که توسط اندازه‌گیری‌های آزمایشگاهی و مقیاس صنعتی ساپورت می‌شود، تکامل یافته است.

3. بررسی مدلسازی چند فازی تاندیش

شبیه سازی عددی عملکرد متالورژیکی تاندیش، همانطور که قبلاً اشاره شد، در دهه هشتاد با یک مدل هیدرودینامیکی دو بعدی (2D) آغاز شد که مدل جبری ویسکوزیته گردابی آشفتگی را در بر می‌گرفت. متعاقباً، مدل‌های سه بعدی، هموژن و آشفته جریان، در ارتباط با معادلات مناسب بقای انرژی حرارتی و ماده و/یا معادلات مسیر ذرات، برای بررسی توزیع‌های زمان ماندگاری (RTD)، انتقال انرژی حرارتی، مسیر ناخالصی ها و غیره توسعه یافتند. مدل‌های دو فازی مبتنی بر مدل‌سازی فاز گسسته (DPM) نسبتاً جدید بوده و عمدتاً برای مطالعه حرکت مایع تحت تاثیر حباب، مسیر حباب‌ها و غیره استفاده می‌شوند. اخیراً، مدل‌های دو فازی و سه فازی جریان‌ها و پدیده‌های انتقال مرتبط گزارش شده‌اند. خلاصه و تحلیل مختصری از این موارد در ادامه ارائه شده است.

Chattopadhyay و همکاران [5-7] مسیر ذرات و حباب را در مدل‌های آب سیستم‌های تاندیش فولادسازی در حالت پایا با اتصال معادلات ناویر-استوکس آشفته به یک مدل فاز گسسته (DPM) بررسی نمودند. در مطالعات آنها، مسیرها، فراوانی و توزیع فاز پراکنده (به عنوان مثال، حباب ها) با دربرگرفتن شکل و قطر ثابت حباب / ذرات محاسبه شد. علاوه بر این، یک مدل تلاطم دو معادله ای برای شبیه سازی پدیده آشفتگی در سیستم به کار گرفته شد. متعاقبا، Chatterjee و همکاران [8] به یک مشکل چالش برانگیزتر پرداخته و به صورت عددی تشکیل چشم باز سیستم تاندیش(TOE) را از طریق یک روش محاسبه ترکیبی VOF (حجم مایع) بعلاوه DPM پیش‌بینی نمودند. در مطالعه آنها [8] جریانهای سرباره از طریق VOF و دینامیک حباب از طریق DPM مدلسازی شدند. شکل TOE پیش بینی عددی شده با مشاهدات در مقیاس کارخانه نظیر مقایسه شد و مطابقت کیفی خوبی بین این موارد برقرار بود. در حالی که یک جریان مایع پر شده از حباب در شرود از پیش فرض شده بود [8]، کار جدیدتر [9] نشان می‌دهد که جریان‌های گاز-مایع در داخل پاتیل می‌تواند پیچیده باشد و جریان مایع پر شده از حباب ممکن است همیشه در طی روش‌های پر کردن پاتیل به سیستم تاندیش غالب نباشد.

در منابع متالورژی، VOF+DPM متصل شده در سال های اخیر رایج بوده است و برای محاسبه جریان گاز-فلز-سرباره در واحدهای فرآوری فولاد استفاده می شود. برای این منظور، لازم به ذکر است که روش‌های محاسبه VOF و DPM بر مفاهیم اساسی متفاوتی تکیه دارند و ممکن است متصل شدن آنها از نظر علمی معتبر نباشد. برای نشان دادن بهتر این موضوع، معادلات حاکم بر اختلاط و حرکت فاز گسسته، در فرمالیسم VOF+DPM متصل شده را می توان در رابطه ای فشرده سازی شده [10] به صورت زیر نشان داد (به بخش 4 نیز رجوع شود):

معادله حرکت اختلاط:

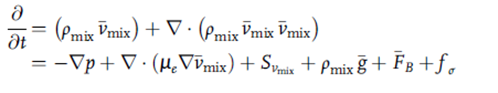
معادله حرکت فاز گسسته:

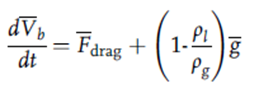
دو معادله قبلی، همانطور که مشاهده شد، به روش صریح از طریق نیروی درگ در واحد حجم و در واحد جرم به هم متصل هستند (توجه شود که نیروی درگ در واحد حجم مایع (FB) و نیروی درگ بر واحد جرم (F_drag) که در دو معادله قبلی ظاهر می‌شوند به هم مرتبط هستند) مانند:

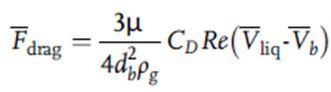
که در آن عدد رینولدز، Re به صورت زیر بیان می شود:

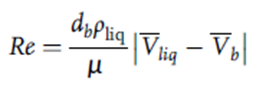
برآورد F_drag (و از این رو، _FB)، همانطور که در معادلات مشاهده می شود، نیاز به سرعت مایع دارد و دومی به روش صریح از معادله جریان (یعنی معادله (1)) شناخته نمی شود. به این ترتیب، مدل _VOF بر اساس یک مقیاس سرعت واحد [11]، یعنی سرعت اختلاط، که از یک وضع پیوسته بر اساس:

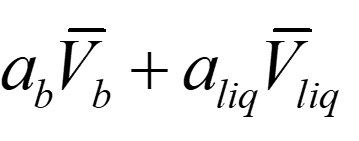
تعریف شده است، فرموله شده است.

در نتیجه، در یک شمای محاسباتی ترکیبی VOF+DPM، مانند آنچه در منابع مهندسی متالورژی به کار می‌رود [8،10]، نیروی درگ در ناحیه پر از حباب (FB) در بهترین حالت می‌تواند بر اساس سرعت اختلاط تخمین زده شود. ادغام سرعت اختلاط، به جای سرعت مایع، برای تخمین نیروهای درگ یک استراتژی یکباره است و به نظر می رسد یک محدودیت جدی فرمول ترکیبی VOF+DPM باشد که در تحقیقات اخیر مورد حمایت و طرفداری قرار گرفته است. واضح است که جریان‌های گاز-مایع که از طریق آزمایشات اندازه‌گیری شده در مدل‌های آبی سیستم‌های پاتیل و عملکرد متالورژیکی تاندیش می‌تواند دید مفیدی ارائه دهد و چنین تقریب هایی را تصدیق کند.

Solorio-Diaz و همکاران[12] و مورالس و همکاران[13] همچنین مدل‌های محاسباتی دو و سه فاز جریان‌ها را در سیستم‌های لدل شرود و توسعه داده‌اند. در کار پیشین [12] پراکندگی ذره رهگیری و حرکت ذرات (ناخالصی) در یک مدل آب مقیاس‌بندی شده از یک هندسه ترکیبی شرود-تاندیش در حالت پایا تحت شرایط غیر همدما که در آن، حرکت فاز گسسته (ناخالصی) از طریق DPM محاسبه شد، مورد بررسی قرار گرفت.

Solorio-Diaz و همکاران[12] و مورالس و همکاران[13] همچنین مدل‌های محاسباتی دو و سه فازی جریان‌ها را در سیستم‌های لدل شرود و سیستم تاندیش توسعه داده‌اند. در کار پیشین [12] پراکندگی ذره رهگیری و حرکت ذرات (ناخالصی) در یک مدل آب مقیاس‌بندی شده از یک هندسه ترکیبی شرود-سیستم تاندیش در حالت پایا تحت شرایط غیر همدما که در آن، حرکت فاز گسسته (ناخالصی) از طریق DPM محاسبه شد، مورد بررسی قرار گرفت. هدف طراحی یک لدل شرود بود که منجر به حذف ویژه ناخالصی از سیستم تاندیش شود. در کار بعدی [13] نویسندگان یک مدل انتقالی، سه فازی، VOF را برای بررسی حباب سرباره در حین تعویض پاتیل در حین عملیات توسعه دادند. از نظر کیفی، نشان داده شد که پدیده‌ کشش سرباره را می‌توان به خوبی از طریق روش محاسبه VOF مدل‌سازی کرد. اگرچه که این تلاش دستاورد بزرگی است اما مدل‌های آن‌ همه ویژگی‌های مشخصه تعویض پاتیل در طول عملیات را در بر نمی گیرد. به عنوان مثال، همانطور که قبلاً اشاره شد، در طول تعویض پاتیل در طول عملیات، یک نرخ خروج تقریباً ثابت از سیستم تاندیش برای تثبیت بهره وری حفظ می شود.

همزمان در حین پر کردن مجدد سیستم تاندیش، دمای مذاب به تدریج با زمان پر شدن تغییر می کند چون فولاد مذاب موجود در پاتیل دمای به مراتب بالاتری نسبت به مذاب موجود در سیستم تاندیش دارد. ​ادغام چنین ویژگی‌هایی در مدل‌های عددی مهم است، زیرا این مدل‌ها را واقعی و قابل انطباق با تحلیل و طراحی فرآیند صنعتی می‌سازد.

Siddiqui و Jha و Alam و همکاران[15] همچنین هیدرودینامیک، فراوانی ناخالصی، مسیرها و همچنین اختلاط گرید را در رویکردهای تطبیقی عملکرد متالورژیکی تاندیش مشابه موارد ذکر شده در بالا بررسی نمودند. در حالی که DPM برای مطالعه مسیرهای ناخاصلی استفاده شد، مدل حجم تنظیم سطح سیال، CLSVOF برای مدل پدیده های اختلاط درجه استفاده شد. در کار بعدی [15] یک معادله پراکندگی رهگیری برای مطالعه اختلاط دو مایع مختلف و قابل اختلاط حل شد که نماینده دو گرید متفاوت فولاد هستند. با این حال، هیچ تلاشی برای اطمینان از دبی جریان نسبتا ثابت از سیستم تاندیش در حین اختلاط، که یکی از ویژگی‌های مهم عملیات ریخته‌گری مداوم است صورت نگرفت. کار اخیر در مورد مدل‌سازی جریان چند فازی حین تعویض پاتیل حین فرآیند کاری، مربوط به تلاش های Zhang و همکاران است [16]. این تیم یک مدل انتقالی، سه فازی، VOF را با در نظر گرفتن مراحل مختلف و کاملاً متفاوت از تعویض حین عملیات، که در شکل 4 نشان داده شده است، توسعه دادند. در حالی که چندین ویژگی تعویض واقعی پاتیل حین فرآیند در مدل آنها گنجانده شده اما دبی ثابت ریخته‌گری و دمای افتراقی (بین مایع ورودی و مایع باقیمانده) در نظر گرفته نشده است.

همانطور که پیش از این اشاره شد، تعویض پاتیل حین عملیات، معمولاً تأثیر قابل توجهی بر سرعت ریخته‌گری ندارد به طوری که نرخ تولید عملاً ثابت می ماند. بنابراین حین تعویض پاتیل و اختلاط گریدی، از آنجایی که پارامترهای فرآیند (به عنوان مثال، نرخ دبی ورودی، حجم سیستم تاندیش و غیره) به صورت دینامیکی تغییر می‌کنند، همیشه تلاش می‌شود تا سرعت ریخته‌گری تقریباً ثابتی را تضمین کند. با این حال، این ویژگی مهم تعویض پاتیل/ عملیات اختلاط گریدی (یعنی نرخ توان تقریبا ثابت) تا کنون در مطالعات شبیه سازی گزارش نشده است. از آنجایی که جریان از سیستم تاندیش به قالب توسط گرانش کنترل می شود، در نتیجه هر چه ارتفاع حمام مذاب در حین پرکردن یا تخلیه سیستم تاندیش تغییر کند دبی جریان نیز تمایل به تغییر دارد. با استفاده از تنظیم مجرای خروجی توسط حرکت استوپر می توان در عمل به دبی ریخته گری ثابتی دست یافت. از آنجایی که جریان از سیستم تاندیش به قالب توسط گرانش کنترل می شود، در نتیجه هر چه ارتفاع حمام مذاب در حین پرکردن یا تخلیه سیستم تاندیش تغییر کند دبی جریان نیز تمایل به تغییر دارد. با استفاده از تنظیم مجرای خروجی توسط حرکت استوپر می توان در عمل به دبی ریخته گری ثابتی دست یافت. مدلسازی یک جامد متحرک همچون استوپر درون دامین جریان پیچیدگی های مدلسازی اضافی خاص خود را دراد و نیازمند ارتقا تکنیک های محاسبتی پیشرفته در برگیرنده مش دینامیک یا متحرک است. علاوه بر این، برای شبیه‌سازی دقیق، تکنیک دوم به گره بندی بسیار ظریف در مجاورت اجسام متحرک نیاز دارد و در نتیجه، محاسبات عددی را سخت‌تر می‌کند.

برای گذشتن از کنار مشکل ذکر شده در بالا و تجسم یک شرط دبی ریخته‌گری ثابت در شبیه‌سازی عددی پدیده‌های اختلاط گریدی، یک روش عددی جایگزین و کارآمد محاسباتی اخیراً توسط Krshnavtar and Mazumdar استفاده شد. در این روش یک الگوریتم ساده پیش‌بینی‌کننده – تصحیح‌کننده فشار (که معمولا به عنوان «الگوریتم تقسیم و حل» شناخته می‌شود) برای استنتاج مجموعه‌ای از همبستگی‌های فشار-زمان از طریق چندین شبیه‌سازی عددی برون خطی استفاده شد. همبستگی‌های به دست آمده در طرح عددی (یعنی کاملا گذرا، رویه VOF دو فازی) به عنوان شرایط مرزی خروجی لازم برای اطمینان از دبی خروج ثابت از سیستم تاندیش ادغام شدند.

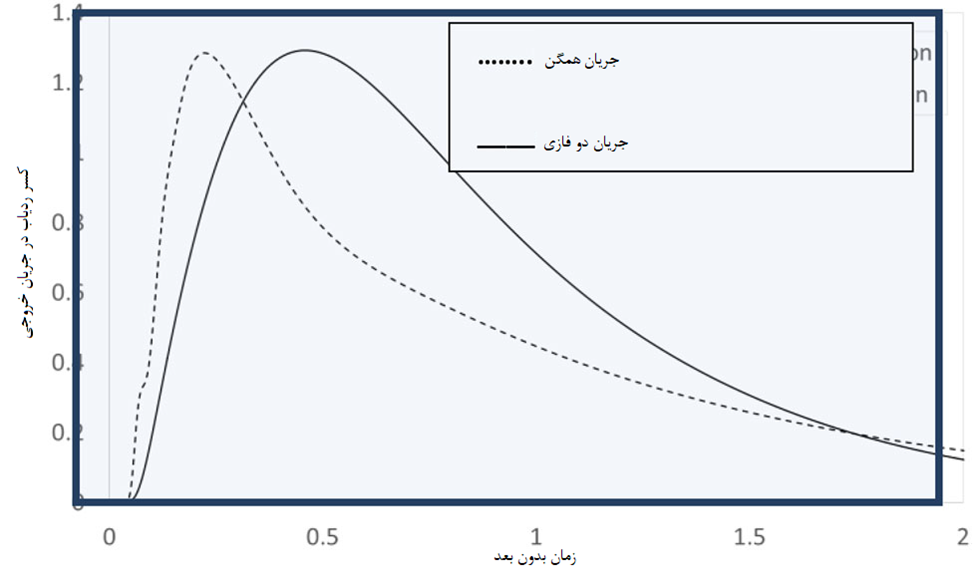
بنابراین، جریان های دو فازی و پدیده اختلاط همراه حین اختلاط گریدی می‌توانست با حفظ دبی جریان خروجی ثابت از سیستم تاندیش بررسی شود. کفایت و مناسب بودن محاسبات آنها به ترتیب در شکل 5 الف و ب نشان داده شده است.

مباحث ارائه شده نشان می دهد که در طول یک دهه گذشته یا بیشتر، شبیه سازی چند فازی سیستم های تاندیش فولادسازی رایج بوده است. هر دو حالت پایا و انتقالی به صورت ریاضی بررسی شده اند. البته تاکید بر حالت پایا بیشتر بوده است. ​تاکنون هیچ مطالعه ای در مورد راه اندازی سیستم تاندیش گزارش نشده است. به طور مشابه، مطالعات مدل‌سازی ریاضی در مورد پدیده‌های انتقال جرم و گرما (به عنوان مثال، اختلاط حرارتی واکنش‌های مایع باقی‌مانده و جدید یا سرباره-فلز و غیره) نیز در منابع وجود ندارد. مهمتر از همه اینکه اعتبارسنجی تجربی نتایج محاسباتی کمتر رایج بوده است. در همین راستا لازم به ذکر است که تلاش های قابل توجهی برای نشان دادن کفایت مدل های جریان آشفته هموژن (از طریق مقایسه مستقیم پیش بینی های عددی با اندازه گیری های تجربی مدل آب پاتیل و سیستم های تاندیش) انجام شد. در مقابل، قابلیت‌های پیش‌بینی روش‌های مختلف محاسبه جریان چند فازی به‌طور دقیق در برابر اندازه‌گیری‌های تجربی معادل ارزیابی نشده‌اند. همچنین ذکر این نکته مهم است که اکثر نشریات تحقیقاتی در مورد عملکرد متالورژیکی تاندیش که در دهه گذشته گزارش شده‌اند، عمدتاً از دانشگاه نشأت گرفته‌اند. در این موارد اطلاعات ساپورت کارگاه های ریخته گری به ندرت با برنامه های مطالعاتی مدل ادغام شده است. شواهد کاربرد مستقیم مدل‌های انتقال مختلف در جهت بهبود عملکرد متالورژیکی تاندیش محدود است. یک رویکرد هم افزا برای بهتر نشان دادن پتانسیل مدلسازی ریاضی (به عنوان یک آنالیزور توانمند فرآیندی، کمک طراحی وبهینه ساز ابزار) نیاز است.

مدلسازی فرآیندهای فولادسازی مستلزم مولتی فیزیک بودن است. مدل‌سازی جامع فرآوری و تصفیه فولاد در کوره‌ها، پاتیل ها، تاندیش‌ها و غیره به طور طبیعی، شبیه‌سازی انواع پدیده‌های هم‌زمان را ایجاب می‌کند که به نوبه خود حل هم‌زمان بسیاری از معادلات دیفرانسیل جزئی غیرخطی متصل شده (PDE) را می طلبد.

برای نشان دادن بهتر این نکته، یک شماتیک از فرآیند تخلیه کوره در شکل 6 ارائه شده است. همانطور که مشاهده می شود، جریان های چند فازی متلاطم (جامد، مایعات و گاز)، ورود و جذب هوا، انتقال گرما و جرم بین فازهای مختلف، ذوب آلیاژها و عوامل تشکیل سرباره، واکنش های شیمیایی و غیره جزء جدایی ناپذیر فرآیند تخلیه کوره هستند. همانطور که تخلیه ادامه می یابد، عمق حمام افزایش می یابد و ارتفاع جریان تخلیه به طور پیوسته با زمان تغییر می کند تا بر شدت جریان در پاتیل تأثیر بگذارد که به نوبه خود بر سرعت جذب هوا، نرخ ذوب و انحلال آلیاژ، واکنش شیمیایی کنترل شده با انتقال جرم و غیره تأثیر گذار است. مشخصا بسیاری از فرآیندهای پیچیده و وابسته به یکدیگر به طور همزمان در حال کار هستند و این مورد در عمل نماینده تمامی عملیات های پالایش و فرآوری انجام شده در BOF ،LF، VD، سیستم تاندیش و قالب است. مدل‌سازی ریاضی جامع فولادسازی به طور طبیعی مستلزم در نظر گرفتن همزمان انواع پدیده‌های فیزیکی و شیمیایی و در نتیجه حل تعداد زیادی از معادلات دیفرانسیل جزئی (PDE) است.

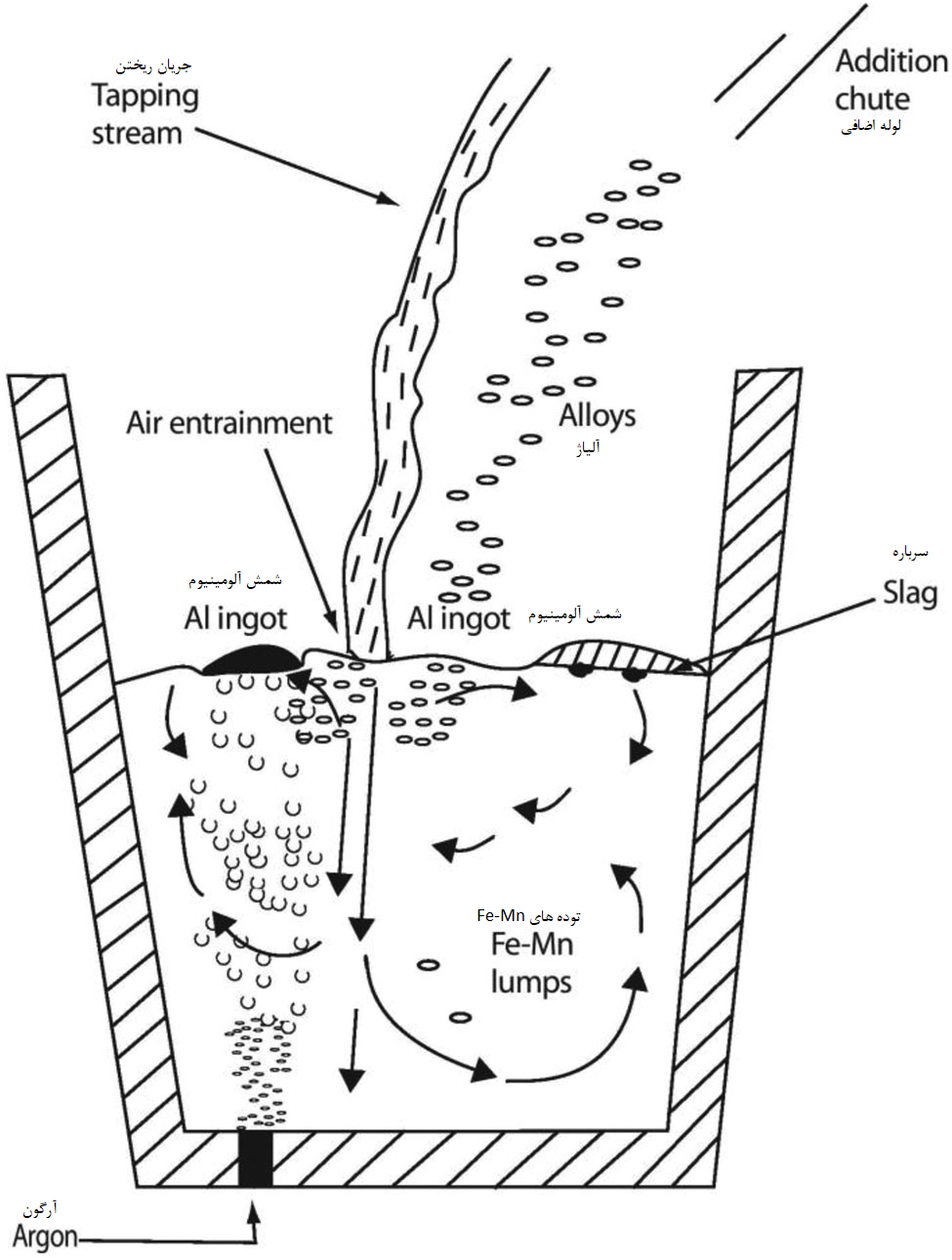
با نگاهی به چنین نقطه‌ای، تعداد PDE‌هایی که برای فرمول‌بندی هر فرآیندی استفاده می‌شوند را می‌توان به عنوان شاخصی از “شمول جامع” هر تحقیق در نظر گرفت. عدد کمتر موجب دقت مدل کمتر است و بالعکس. بنابراین، مدل‌سازی جریان آشفته در سیستم تاندیش در حالی که شامل حل تنها پنج یا شش PDE، شبیه‌سازی جامع عملیات سیستم تاندیش مربوط به جریان‌های چند فازی، انتقال گرما و جرم، واکنش شیمیایی و غیره است، ممکن است از طرف دیگر نیاز به حل عددی تعداد زیادی معادلات دیفرانسیل جزئی داشته باشد. پر واضح است که بسیاری از روابط کمکی و ضرایب تجربی (به عنوان مثال، ضریب تبادل تکانه بین فازی، نیروهای کشش سطحی، شار حرارتی، ویسکوزیته موثر و غیره)، علاوه بر PDEهای حاکم، برای فرموله کردن مدل‌های فرآیند در فرم بسته این مدل ها مورد نیاز است.

بر اساس بحث قبلی، یک پارامتر “AIM” (شاخص پیشرفت مدل‌سازی) در اینجا برای تجسم پیشرفت در مدل‌سازی در مقیاس کمی معرفی شده است. AIM به عنوان نسبت تعداد PDE های حل شده در هر پژوهش به تعداد PDE های مورد نیاز برای فرمول بندی پدیده جریان دو بعدی، همگن و آشفته (یعنی برابر پنج (مقدار مرجع)) تعریف می شود. همانطور که قبلا ذکر شد، مقدار کوچکتر AIM نشان دهنده مدل سازی ساده و شبیه سازی عددی در بهترین حالت یک یا دو پدیده و بالعکس است. مقدار عددی AIM نماینده مطالعات مدلسازی ریاضی گزارش شده در بازه زمانی 1985-2018 در شکل 7(a) نشان داده شده است. همانطور که مشاهده می شود، به نظر می رسد AIM در محدوده 2-1 قرار دارد که به ندرت از 2 بیشتر است، برای اکثریت قریب به اتفاق مطالعات. این بدان معناست که همچنان به اندازه کافی توسعه خلاقانه در این زمینه صورت نگرفته و هنوز جای پیشرفت های دیگری نیز وجود دارد.

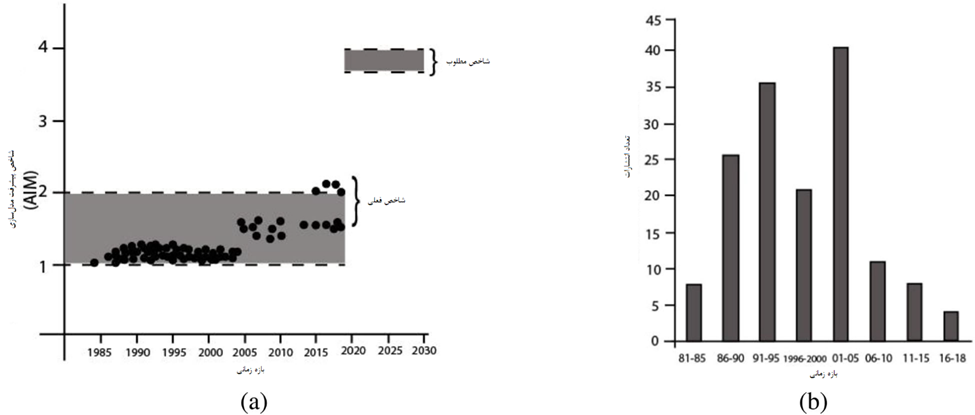
جالب توجه است، اگر فراوانی انتشارات آرشیو شده در مورد عملکرد متالورژیکی تاندیش به صورت گرافیکی (شکل 7b) به عنوان تابعی از هر پنج سال، در بازه زمانی 1985-2018 ارائه شود، تصویر کمتر اقناع کننده ای ظاهر می‌شود. تعداد انتشارات و در نتیجه تحقیقات در مورد عملکرد متالورژیکی تاندیش در طول دهه گذشته به تدریج کاهش یافته است. کاهش تعداد مراکز تحقیقاتی متالورژی فرآیند در سراسر جهان و همچنین عدم علاقه به موضوع آهن و فولادسازی به نظر می‌رسد که دلایل اصلی منتهی به سناریوی حاضر باشد. این یک موضوع مهم است و در چند وقت اخیر در چندین فروم مختلف تکرار شده است.

4. مدلسازی جریانها و انتقال حرارت در عملکرد متالورژیکی تاندیش

به جز تعداد معدودی، در اکثر مطالعاتی که تاکنون در مورد عملکرد متالورژیکی تاندیش گزارش شده است یک جریان مذاب همگن در لدل شرود در نظر گرفته شده است؛ اما ممکن است همیشه اینطور نباشد. در بسیاری از کارخانه‌های فولاد، آرگون به‌طور معمول به داخل شرود تزریق می‌شود و در نتیجه یک مخلوط دو فازی و گاز-مایع به جای مذاب همگن ایجاد می‌شود. تحت چنین شرایطی، برهمکنش‌های دو و یا سه فاز (متال-گاز) در مقیاس بزرگ می‌توانند در سیستم تاندیش ایجاد شوند و این به نوبه خود می‌تواند بر جریان مذاب، سرعت واکنش سرباره-فلز، ناحیه چشم باز سیستم تاندیش (TOE) و غیره تأثیر بگذارد. در ادامه، کارهای اخیر نویسنده حاضر و همکارانش در مورد جریانات در پاتیل، چه با و چه بدون دمش آرگون، و تأثیر متعاقب آنها بر عملکرد متالورژیکی تاندیش و عملکرد هیدرودینامیکی سیستم تاندیش(RTD در تاندیش و افت دما در شرود) به اختصار ارائه شده است.

4.1. مدل‌سازی تزریق آرگون در لدل شرود و تأثیر متعاقب آن بر عملکرد متالورژیکی تاندیش و عملکرد هیدرودینامیکی سیستم تاندیش

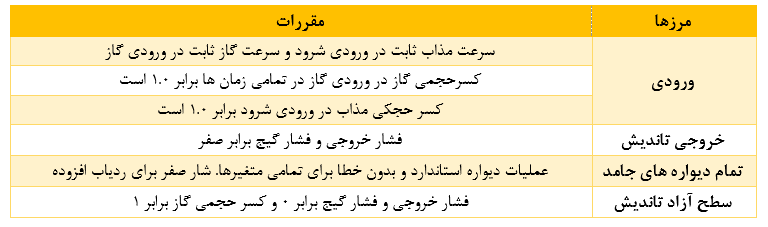
برای بررسی نقش تزریق گاز به پاتیل و تأثیر متعاقب آن بر هیدرودینامیک سیستم تاندیش و پدیده‌های RTD، یک روش محاسبه VOF گذرا توسعه داده شده است و سیستم‌های تاندیش ریخته‌گری سه رشته‌ای که در جدول 2 (کارخانه های E و F) توضیح داده شده‌اند به عنوان کیس استادی در نظر گرفته شده است. در ابتدا، محاسبه ایزوترم بدون سرباره انجام شده است که در آن، نرخ تزریق حجمی آرگون، به دمای میانگین 1873 کلوین و 1 درجه تعدیل شده است. فشار اعمال شد. معادلات حاکم بر پیوستگی، حرکت، توربولانس و اختلاط مواد در نماد تنسور فشاری به صورت زیر نمایش داده می شوند:

معادله پیوستگی:

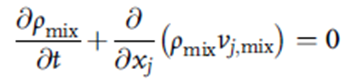
معادله بقای مومنتوم:

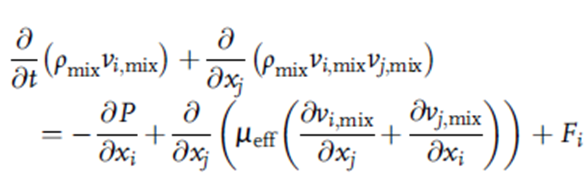
در بالا، vi، mix و vj، mix  سرعت اختلاط میانگین زمانی شده به ترتیب در جهات i_th و j_th می باشد و P فشار دینامیکی است که به فشار هیدرواستاتیک موضعی (لوکال) باز می گردد.

F_i نرخ انتقال مومنتوم حجمی اضافی ناشی از نیروهای کشش سطحی را نشان می دهد. برای این منظور، نسخه های استاندارد موجود در ANSYS Fluent [20] استفاده شد. چگالی مخلوط، ρ_mix، که در رابطه (5) و (6) ظاهر می شود، از قانون اختلاط تخمین زده می شود و به صورت زیر بیان می شود:

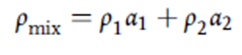
در رابطه (7) پسوند 1 و 2 به ترتیب بیانگر دو فاز موجود در سیستم یعنی هوا و آب یا فولاد و آرگون است. کسر حجمی فاز اولیه (به عنوان مثال، فاز 1)، با حل یک معادله انتقال ادوکشن حجم اضافی به دست می آید که به صورت زیر نمایش داده می شود:

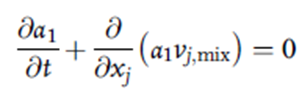
بر این اساس، کسر حجمی فاز ثانویه، یعنی فاز 2، از معادله زیر به دست می آید:

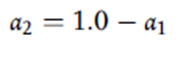
معادلات RANS (Reynolds Average Navier-Stokes) ارائه شده در بالا، ویسکوزیته موثر، μeff = (μ+μ_t) را نشان می دهد و این پارامتر اخیر، در مطالعه حاضر از ضریب استاندارد مدل آشفتگی k-e برآورد شده است. مطابق مدل توربولانس k-ε داریم:

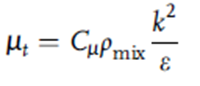
انرژی جنبشی آشفتگی k و نرخ اتلاف آن ε که در رابطه (10) ظاهر می‌شود با حل دو معادله نوع انتقال اضافی محاسبه می‌شوند که به ترتیب، بقای انرژی جنبشی آشفتگی خاص  (k) و نرخ اتلاف آن (ε) را بیان می‌کنند.

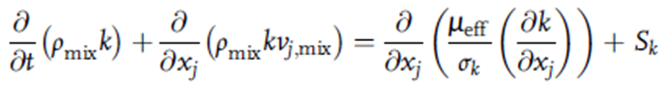
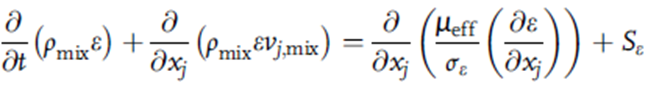
در بالا Sk = G – ρ_mix ε که در آن، G نرخ حجمی تولید توربولانس ناشی از کار برشی در برابر گرادیان سرعت متوسط است. این مورد به صورت ریاضی مطابق زیر نشان داده می شود:

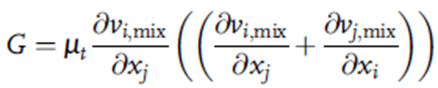
ترم منبع S_ε که در معادله 12 ظاهر می شود به صورت زیر قابل تعریف است:

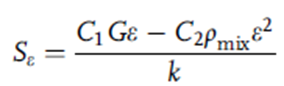
پنج ثابت تجربی، یعنی c₁. c₂; c_μ; σ_k و σ_ε که در معادله (10) تا (14) ظاهر می شوند به ترتیب به مقادیر استاندارد آنها، یعنی 1.44، 1.92، 0.09، 1 و 1.30 اختصاص داده می شوند.

علاوه بر موارد فوق، یک معادله انتقال اسکالر برای استنباط “منحنی C” (که اساساً تغییر غلظت با زمان در خروجی سیستم تاندیش را به تصویر می‌کشد) به صورت عددی و در نتیجه آن، پارامترهای توزیع زمان ماندگاری (RTD) مربوط حل شد. یک عبارت مناسب نشان دهنده بقای جرم قسم اضافه شده “s” از طریق عبارت زیر ارائه می شود:

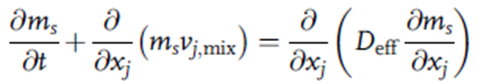
در معادله (15)،  Deffحاصل جمع انتشار مولکولی و آشفته (D+D_t) است و از تئوری توربولانس استنباط می شود، با فرض اینکه عدد اشمیت توربولانت، μ_eff/(ρ_lDeff)، واحد باشد، یعنی انتشار توربولانت به صورت عددی برابر است با ویسکوزیته جنبشی گردابی، μ_t/ρ_l.

افزودن پالس ردیاب به سیستم تاندیش از طریق حل عددی معادله (15) شبیه سازی شد. به دلیل جفت شدن یک طرفه، ابتدا فیلد جریان محاسبه شد و بر اساس فیلدهای جریان و آشفتگی همگرا، معادله پراکندگی ردیاب (به عنوان مثال، معادله (15)) حل شد. از تغییرات پیش‌بینی‌شده غلظت با زمان، “منحنی C” استنتاج شد. شرایط اولیه و مرزی قابل اعمال برای معادلات دیفرانسیل حاکم در جدول 4 خلاصه شده است.

هندسه سیستم تاندیش، ابعاد پوشش و پارامترهای عملیاتی مربوطه در جدول 5 ارائه شده است، در حالی که توزیع میانگین زمان پیش بینی شده عددی کسرهای حجم فاز در پوشش در شکل 8a نشان داده شده است. این مورد به وضوح یک منطقه آزاد از جت مایع را نشان می دهد که به دنبال منطقه جریان مخلوط گاز-مایع شدید، فراتر از طول شرود به داخل سیستم تاندیش گسترش می یابد.

نتایج تجربی معادل نشان داده شده در شکل 8b پیش بینی های مدل را به خوبی تایید می کند. نکته جالب این است که در غیاب تزریق آرگون و نشت هوا، شرود تمایل به پرشدن کامل با مایع را دارد و در نتیجه جریان مایع همگن در طول شرود مطابق شکل 7c می شود.

تأثیر گاز شرود بر عملکرد متالورژیکی تاندیش و بر عملکرد هیدرودینامیکی سیستم تاندیش نیز همچنین از موارد مهم است. برای بررسی این موضوع، ابتدا محاسبات جریان همگن انجام شد و جریان‌های پیش‌بینی‌شده در دو صفحه مختلف سیستم تاندیش به ترتیب در شکل 9a و b نشان داده شده‌اند. این موارد حضور قابل توجهی از جریان مستقیم رو به بالا در سیستم تاندیش را در غیاب هر گونه تزریق گاز در شرود نشان می دهد. در مقابل، نتایج معادل که از طریق VOF استنتاج شده‌اند (یعنی با در نظر گرفتن جریان همزمان آرگون و فولاد در شرود) و نشان داده شده در شکل 10 نشان‌دهنده تأثیر قابل‌ توجه تزریق آرگون بر جریان مایع وارد شده در سیستم تاندیش است.

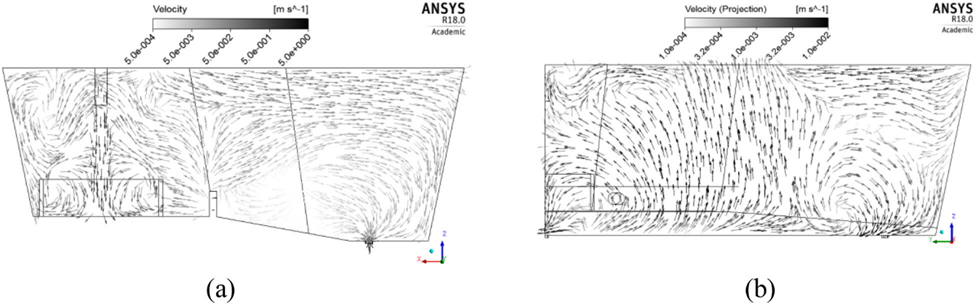
در آنجا، شناور بودن حباب های گاز به وضوح دیده می شود که نفوذ جت مایع ورودی به داخل مذاب را محدود می کند. این به نوبه خود حرکت رو به پایین مایع را به تعویق می اندازد تا نسبت به جریان هایی که در شکل 9 ارائه شده اند تا حدودی متفاوت و کند شود. منحنی های C متناظر سرتاسری، با و بدون تزریق آرگون، که در شکل 11 ارائه شده است، به وضوح تأثیر قابل توجهی از تزریق گاز بر پدیده RTD حاصل را نشان می دهد. همانطور که مشاهده می شود، تزریق آرگون در شرود یک “منحنی C” پراکنده تر ایجاد می کند (که به معنای جریان پراکنده تر پلاگ به خرج حجم های جریان به خوبی مخلوط شده است) که به ترتیب با الگوهای جریان ارائه شده در شکل 9 و 10 مطابقت دارد. بر اساس چنین مواردی، می توان پیش بینی کرد که تزریق گاز در شرود احتمالا بر عملکرد متالورژیکی سیستم های تاندیش فولادسازی تأثیر می گذارد. چنین روندهای محاسباتی در حال حاضر از طریق آزمایش های مدل آب مورد بررسی قرار می گیرند.

4.2. مدل سازی افت دمای مذاب در لدل شرود

سه نوع مختلف طرح‌های لدل شرود صنعتی در شکل 12 نشان داده شده‌اند. در آنجا، طرح‌های (b) و (c) دارای ویژگی‌هایی هستند که برای رساندن گاز شرود (عموما آرگون) به بیرون، در مجاورت اتصال شرود-صفحه جمع کننده طراحی شده‌اند. در مقابل، آرگون مستقیما در طرح (d) داخل شرود تحویل داده می شود و همراه با فولاد مذاب به داخل سیستم تاندیش منتقل می شود.

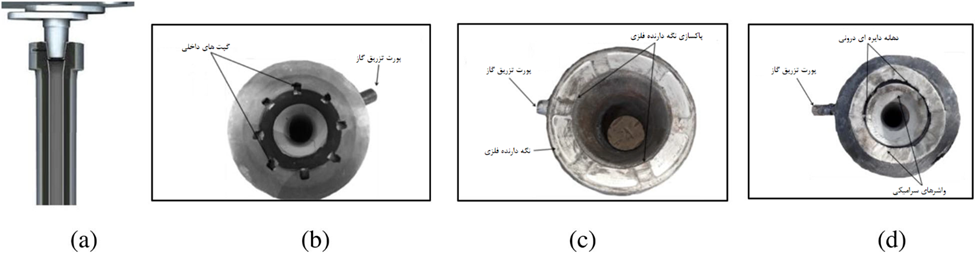
نتایج مدل‌سازی فیزیکی ارائه‌شده در جاهای دیگر نشان می‌دهد که شرودغوطه‌ور شده از نوع (b) و (c)، در غیاب هر گونه نفوذ هوا، به طور کامل پر می‌ماند و یک جریان توربولانت همگن از فولاد مایع در داخل شرود در طول انتقال پاتیل به سیستم تاندیش، همانطور که در شکل 13a نشان داده شده است، ایجاد می‌شود.

عبور فولاد مذاب از یک شرود می‌تواند باعث اتلاف حرارت قابل توجه از سطح خارجی  شرود به میزان 0.1-0.2 MWm^-2 باشد. در نتیجه دمای مذاب می تواند بین پاتیل و سیستم تاندیش کاهش یابد. در حالی که مدل‌سازی جریان همگن در ارتباط با این موضوع ناچیز است، آگاهی از افت دمای ایجادشده از همین موضوع حین پر ​شدن به ویژه برای مطالعه پدیده‌های انتقال حرارت در سیستم تاندیش و قالب مهم است. در این راستا، به ندرت شبیه‌سازی‌های مقیاس صنعتی که توسط اندازه‌گیری‌های مقیاس کارخانه ساپورت شوند، در منابع گزارش شده‌ است.

برای تعیین کمیت میزان افت دما در طول انتقال مذاب از پاتیل به سیستم تاندیش از طریق یک شرود، یک مدل جریان آشفته سه بعدی، حالت پایدار و همگن ایجاد شد. این مورد به یک معادله موازنه انرژی حرارتی حالت پایدار برای پیش‌بینی توزیع دما بر روی دامین شرود در هم آمیخته شامل شرود جامد و نواحی مذاب کوپل شد. معادلات حاکم قابل اعمال برای جریان توربولانت همگن و انتقال حرارت به خوبی شناخته شده است و بنابراین، در اینجا مجددا ارائه نمی شود. در این مورد شرایط مرزی حرارتی وابسته به فاصله بر روی سطح شرود اعمال شد تا انواع مختلف محیط‌هایی را که شرود در عمل در معرض آن قرار می‌گیرد، در نظر بگیرد (شکل 13a). برای این منظور، شرایط مرزی تشعشع، با دمای محیط 298 و 1073 کلوین، به ترتیب بر روی مناطق A و B اعمال شد و این در حالی است که سطح غوطه‌ور شده شرود عایق‌ فرض شده است (یعنی اساسا دمای ذوب در نظر گرفته می‌شود).

شرایط مرزی ورودی در مورد جریان و دما بر اساس نرخ ریخته گری و دمای بالا بردن پاتیل حین ایجاد شرایط مرزی جریان خروجی در انتهای شرود اعمال شد. محاسبات عددی از طریق ANSYS CFX انجام شد که در آن نماینده های: چگالی، رسانش حرارتی و گرمای ویژه شرود، که از تجزیه و تحلیل دقیق داده‌های موجود در منابع استنتاج شده بود، اعمال شد. به طور مشابه، مقاومت‌های حرارتی ویژه شرود با گرید مناسب در فولاد مذاب جاری برآورد شد و در شماتیک حل عددی برای محاسبه توزیع دما در هندسه شرود-مذاب در هم آمیخته گنجانده شد. در اینجا ذکر این نکته ضروری است که تخمین مقاومت های تماس حرارتی با استفاده از اندازه گیری ها در ابعاد کاری کارخانه و تبدیل به تئوری تکبعدی رسانش حرارتی شعاعی در هندسه استوانه ای به دست آمده است. خصوصیات و پارامترهای مورد استفاده در شبیه سازی عددی در جدول 6 خلاصه شده است.

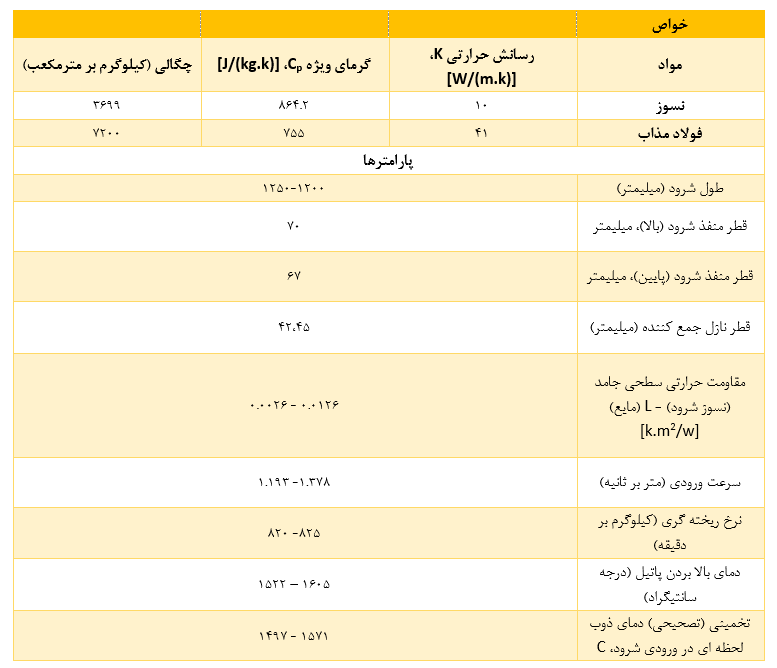
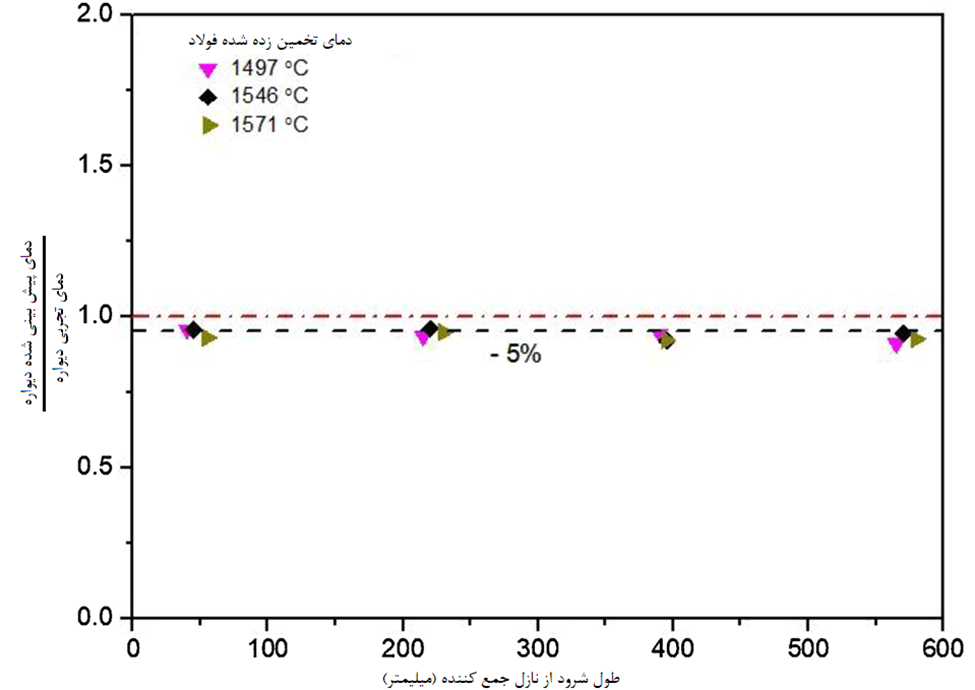
در بالای شرود در حال استفاده (به عنوان مثال، شکل 13b، اواسط مسیر ریخته گری، دمای سطح در چهار مکان مختلف توسط یک پیرومتر مادون قرمز اندازه گیری شد و نتایج به دست آمده به طور مستقیم با پیش بینی عددی مربوطه مقایسه شده است. این داده ها در شکل 14 نشان داده شده است.

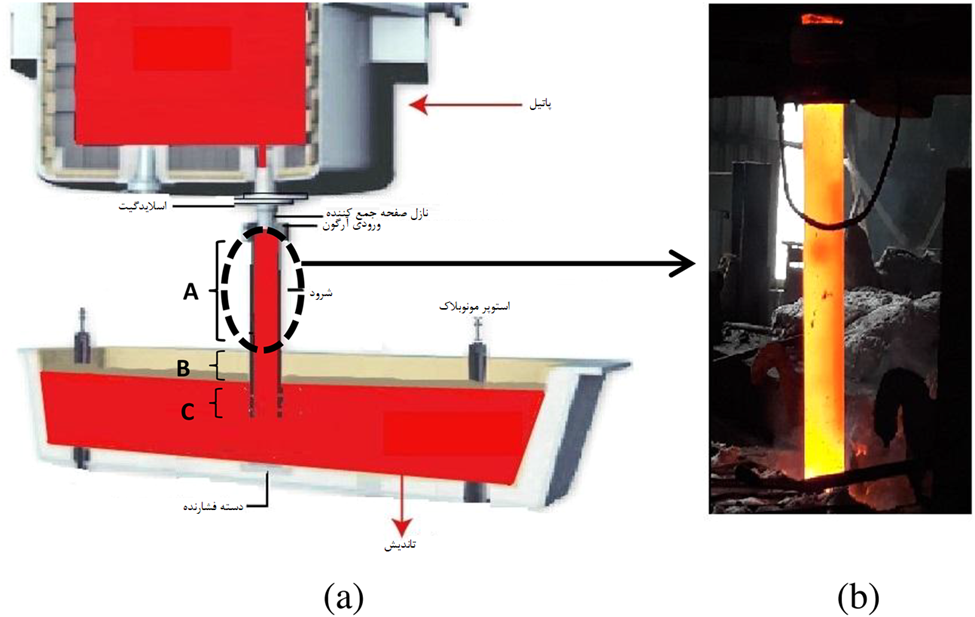
در موارد زیر مطابقت بسیار خوبی مشاهده می شود (عمدتا در محدوده 5٪ و بیشتر):

• عدم قطعیت متعاقب عدم تراز شرود در عمل
• واکنش های بین دیرگداز و فولاد که بر خواص ترموفیزیکی شرود تأثیر می گذارد
• تقریب های مورد استفاده در تخمین دمای فولاد مذاب در ورودی شرود

با این حال، مهم‌تر از همه، مطالعه حاضر نشان می‌دهد که تقریباً 2 تا 3 درجه سانتی‌گراد افت دما محتمل است، زیرا جریان‌های فولاد مذاب حین ریخته‌گری بلوم صنعتی با سرعت تقریبی 800 کیلوگرم در دقیقه به پایین شرود به طول تقریبی 1200 میلی‌متر حرکت می‌کنند. تمرین مشابهی از طریق یک روش محاسبه VOF در حال حاضر برای بررسی افت دمای مذاب و افزایش دمای گاز حین جریان فولاد-آرگون از طریق شرود از پاتیل به سیستم تاندیش در حال انجام است.

5. خلاصه

 در حال حاضر حجم چشمگیر منابع در مورد مدل‌سازی ریاضی سیستم‌های تاندیش فولادسازی در دسترس است. این نشان می‌دهد که اکثر تحقیقات، گزارش‌شده در طول سال‌های 1985-2000، به مدل‌سازی جریان فولاد مذاب در سیستم‌های تاندیش محدود شده‌اند که در آن، حضور سرباره، آرگون/هوا و غیره به طور کلی نادیده گرفته شده است. علاوه بر این، تأکید بر مدل‌سازی جریان، RTD، شناوری ناخالصی، و توزیع انرژی حرارتی در طول دوره عملیاتی ثابت یک سیستم تاندیش بوده است. سیستم تاندیش فولادسازی یک سیستم جریان چند فازی را نشان می‌دهد و از این رو مدل‌سازی عددی جامع متالورژی سیستم تاندیش نیاز به یک مدل جریان توربولانت انتقالی، واکنش‌دهنده، غیر همدما و چند فازی دارد. با توجه به منابع موجود کنونی اشاره شده است که شبیه‌سازی موثر عملیات های مختلف متالورژی سیستم تاندیش که در هنگام راه‌اندازی، حالت پایدار و همچنین عملیات پایان توالی با آن مواجه می‌شوند، امکان‌پذیر است. بررسی منابع نشان می‌دهد که مدل‌سازی چند فازی سیستم‌های تاندیش فولادسازی در سال‌های اخیر (2008 به بعد) آغاز شده است و تاکنون مدل‌های دو فازی و سه فازی از پدیده‌هایی مانند اختلاط گرید، حباب سرباره، تشکیل چشم سیستم تاندیش و غیره تنها توسط چند گروه از محققین توسعه داده شده است. علی رغم وجود رویه‌ها و نرم‌افزارهای عددی قدرتمند، پیشرفت در مدل‌سازی در دهه گذشته تا حدودی کند بوده است. کاهش تعداد مراکز تحقیقات فرآیند در سراسر جهان و عدم علاقه به پیگیری تحقیقات فولادسازی دو دلیل اصلی چنین روندی به نظر می رسد. همچنین ذکر شده که اتکا به اندازه‌گیری‌های تجربی برای اثبات پیش‌بینی‌های مدل ریاضی با گذشت سال‌ها کاهش یافته است. ادغام ویژگی‌های فرآیند واقعی در مدل‌سازی عددی یک گام مهم است و این مورد اکثرا و خصوصا در زمینه مدل‌سازی فرآیندهای فولادسازی با دمای بالا دشوار است. برای برجسته کردن این موضوع، انتقال آرگون شرود ​از پاتیل به سیستم تاندیش به عنوان مثال در نظر گرفته شده و به طور خلاصه بر نقش اندازه‌گیری‌های مقیاس آزمایشگاهی و صنعتی در توسعه مدل تأکید شده است.

برای کسب اطلاعات بیشتر با ما در تماس باشید.