نیم نازل ریخته گری مداوم فولاد و بررسی تاثیر دمش گاز آرگون در آن(مقایسه شبیه‌سازی‌های جریان عددی با اعتبارسنجی مدل آبی)

در این مقاله تاثیر حباب های گاز خنثی ناشی از دمش گاز آرگون در نیم نازل ریخته گری مداوم (S.E.N) بر جریان قالب بررسی می شود. نتایج مدل فیزیکی با نتایج شبیه سازی جریان عددی متناظر آن مقایسه می شود. در مدل های عددی، سرعت حباب ها با محاسبه تعادل نیرو بین نیروی شناوری، نیروی درگ (drag) و سایر نیروها موثر بر حباب ها مشخص می شود. برای سایز حباب های موجود در مدل فیزیکی، سرعت بالا آمدن حباب های مشخص شده در مقایسه با مدل آزمایشی آب بسیار بیشتر است. عوامل متفاوتی می تواند بر سرعت بالا آمدن حباب ها تاثیرگذار باشد. یکی از این موارد حضور توربولانس (آشفتگی جریان) است که به وضوح سرعت بالا آمدن را کاهش می دهد. تاثیر مدل های توربولانس و اصلاح درگ حباب تحت توبولانس در شبیه سازی جریان عددی تحلیل و با نتایج مدل آب مقایسه می شود.

1. مقدمه:

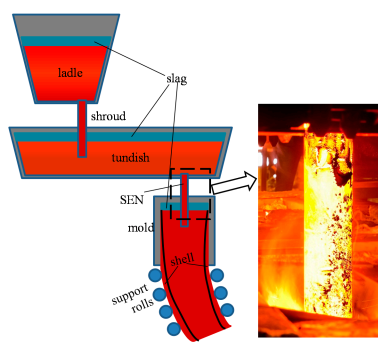
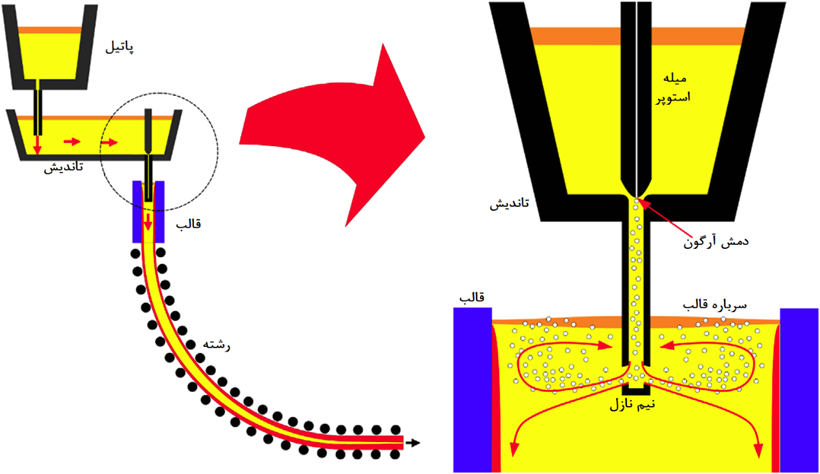
تزریق گاز در نوک میله استوپر در ریخته گری مداوم اقدامی رایج در جلوگیری از گرفتگی و کنترل کیفیت فولاد تولیدی است. گاز دمیده شده حباب هایی را تشکیل می دهد و توسط فلز مذاب از میان نیم نازل ریخته گری مداوم (نازل غوطه‌وری) عبور نموده و به ناحیه قالب می رسد (شکل1). اغلب حباب های گاز به سطح قالب می آیند و از فلز مذاب در این محل خارج می شوند.

در یک سیال راکد، هر حباب گاز به تنهایی شروع به بالا رفتن می کند و به یک سرعت حداکثری می رسد که در این سرعت ثابت تعادل بین نیروی درگ و نیروی شناوری برقرار است. اساسا سرعت بالا آمدن نهایی برای حباب‌های بزرگتر بیشتر است. نیروهای درگ و سرعت نهایی بالا آمدن در مذاب برای بالا آمدن حباب ها در آب و همچنین در مذاب مطابق شکل 2 بررسی شده است. شکل ناپایدار حباب ها بر خلاف کره هایی صلب، موجب اثر شبه اشباع می شود و سرعت بالا آمدن نهایی فقط برای حباب های بیشتر از 2 میلی متر کمی افزایش می یابد. در نتیجه حباب های 2 تا 30 میلی متر سرعت نهایی بالا آمدن بین 0.2 تا 0.3 متر بر ثانیه دارند که در واقع خیلی کمتر از کره های صلب با همان سایز و چگالی است. با این وجود، قوانین درگ برای ذرات صلب در شبیه سازی های عددی حباب های گاز به کار می رود. تفاوت بین تنش سطحی مذاب در سرعت نهایی بالا آمدن تاثیر و تفاوت چندانی ایجاد نمی کند. سایز حباب در جریان قالب در شرایط ریخته گری در عمل به فرآیند دمش گاز و به انتقال از محل دمش (معمولا در بالای نیم نازل ریخته گری مداوم) به قالب بستگی دارد. تعیین دقیق سایز حباب ها و رفتار حرکتی در شرایط ریخته گری عملی دشوار است. آزمایش های عملی شرایط جریان در ترکیب با فلز مذاب کاهش مقیاس یافته و یا همچنین مقیاس خود را (معمولا با ضریب 3) در مایع از دست می دهد.این مدل باید ساختار جریان در نیم نازل ریخته گری مداوم و قالب را ارائه دهد. محدوده های شباهتی می تواند به بررسی اینکه آیا می توان با انتخاب پارامترهای فرآیند مناسب به همان وضعیت جریان در ستاپ آزمایشگاهی رسید کمک کند. تفاوت اساسی میان شرایط واقعی و مدل فیزیکی می تواند به دلیل احتمال تفاوت بین مقیاس هندسی، تفاوت تنش سطحی و سطوح فشار مطلق باشد [1-6]. به دلیل این تفاوت ها، سایز حباب ها ممکن است در مقایسه با شرایط واقعی متفاوت باشد. در نتیجه، اطمینان از شباهت داده های شرایط عملی و آزمایشگاهی دشوار است.

در شبیه‌سازی عددی جریان قالب، فرآیند دمش عمدتا در نظر گرفته نمی‌شود و بنابراین، اندازه حباب و توزیع چگالی در شرایط مرزی جریان ورودی در مقطع نیم نازل ریخته گری مداوم مورد نیاز است. در بسیاری از موارد سایز حباب با استفاده از قانون درگ برای به دست آوردن میزان رانش حباب انتخاب می شود. سایز حباب با اندازه گیری مدل آبی بدون بعد [7] یا کوچک [8]تعیین می شود؛ مشاهده و اندازه گیری توزیع حباب در مدل آبی انجام می شود و انتخاب سایز حباب در مدل شبیه سازی به نحوی است که به بهترین شکل با شرایط آزمایش متناسب شود [9]؛ سایز حباب مطابق حباب های منجمد شده در فلز ریخته گری انتخاب می شود؛ سایز حباب با روش “اثر منطقی” حباب های گاز بر جریان [10] و یا بدون هیچگونه اعتبارسنجی آزمایشگاهی انتخاب می شود [4].

به همین ترتیب، در برخی شبیه‌سازی‌ها، سرعت بدون محاسبه سرعت رانش در شبیه‌سازی مشخص می‌شود[7].  سرعت جریان گاز دمیده شده در شرایط ریخته گری معمولاً در دبی حجمی در شرایط استاندارد (دمای اتاق و فشار اتمسفر) مشخص می شود. با داشتن دمای مذاب فولاد اگر دمای گاز نیز همان میزان فرض شود باید تقریبا با ضریب 6 منبسط شود (1800 K/300 K = 6).

فشار هیدرواستاتیک فولاد مذاب داخل نیم نازل ریخته گری مداوم در ارتفاع سطح قالب تقریبا برابر با فشار اتمسفر است. 30 سانتی متر زیر سطح قالب (عمق نفوذ معمولی برای حباب های گاز با قطر چند میلی متری در جریان های قالب) ضریب انبساط حدود 5، در حالی که این عدد در فاصله 700 میلی متر بالای سطح قالب (موقعیت معمول برای تزریق گاز در ناحیه بالای نیم نازل ریخته گری مداوم) حدود 12 است.

برخی از محققین از ضریب انبساط 6 [7]، برخی از ضریب پایین تر، به عنوان مثال ضریب 4.1 (رفرنس [11]) استفاده می کنند و برخی دیگر نرخ دمش مدل را با همان نرخ در ریخته گری واقعی مرتبط نمی دانند.

حرکت حباب ها در جریان آشفته نسبت به یک مایع راکد پیچیده تر است: همانطور که دررفرنس [12] گزارش شده، آشفتگی جریان سرعت بالا آمدن را کاهش می دهد [13,14]، نه اینکه بدون تاثیر باشد [15,16] و یا اینکه افزایشی ایجاد کند [17].

مکانیسم های این پدیده ها تاکنون تا حد کمی شناخته شده است. بنابراین، مدل های ریاضی توسعه داده شده برای توصیف این پدیده ها غالبا بر پایه روابط تجربی است. کاهش سرعت حباب در هنگاهم توربولانس در یک جریان مشابه قالب توسط Kwon و همکاران مشاهده شد [18] و مدل Brucato [14] (شکل ₂a) برای در نظر گرفتن این پدیده در شبیه سازی جریان عددی استفاده شد. آزمایشات نشان داده که در جریان آشفته خود حباب های موجود نیز باعث افزایش توربولانس می شود [19]. مدل ساتو [20] یک ترم ویسکوزیته گردابی اضافی متناسب با کسر حجمی حباب و سرعت اضافه می‌کند و اغلب برای شبیه‌سازی‌ جریان قالب با دمش حباب به کار می رود [9،21-23].

اگرچه در سایزهای بزرگ حباب ها پارامتر اندازه بر سرعت رانش تاثیر چندانی ندارد، اما در برخی تحقیقات پارامتر سایز نیز به دلیل در نظر گرفتن ادغام و شکسته شدن حباب ها در نظر گرفته می شود [21،22].

2. مدل سازی ریاضی

2.1. مدل سازی توربولانس

در بسیاری از شبیه‌سازی‌های قدیمی و نوین، از مدل توربولانس k–ε برای مدل‌سازی توربولانس فاز مایع یا مخلوط مایع و گاز استفاده می‌شود. اخیرا برخی از تیم های تحقیقاتی از شبیه‌سازی‌های گردابی بزرگ برای شبیه‌سازی جریان قالب چند فازی استفاده نموده اند [8،23،25-27]، لازم به ذکر است مدل‌های توربولانس ترکیبی مانند مدل شبیه‌سازی تطبیقی مقیاس (SAS) به ندرت به کار می رود[23].

برای نتایج ارائه شده در این تحقیق، از دو مدل توربولانس استفاده شده است:  k-ε[28،29] قابل دستیابی (RKE) و مدل SAS [29-31].

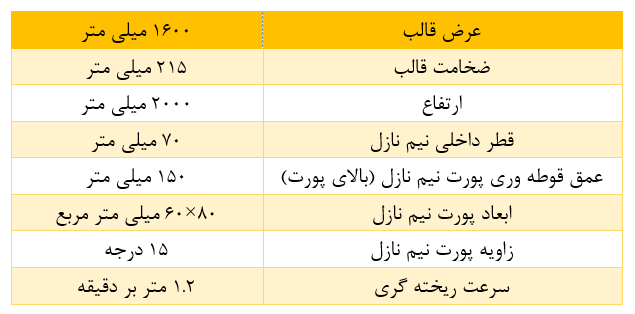
هر دو مدل برای محاسبه جریان تک فاز انتقالی در مدل آب موجود در قالب برای مقایسه با اندازه‌گیری‌های جریان تک فاز در «قسمت توضیحات اکسپریمنتال» آورده شده است. بنابراین، شکل هندسی قالب معادل مدل آب است (ابعاد آورده شده در جدول 1) و به عنوان مثال، انجماد (مطابق رفرنس [32]) در نظر گرفته نشده است.

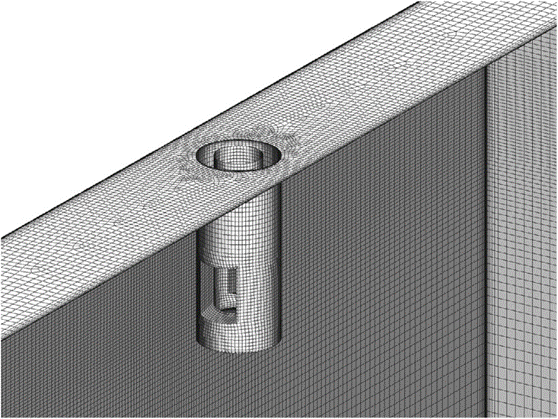
شکل 3 شبکه مورد استفاده برای هر دو شبیه سازی را با اندازه سلول 5 میلی متر با لایه های مرزی 0.3 میلی متر در دیواره های داخلی نیم نازل ریخته گری مداوم، هم در وجوه وسیع و هم کم پهنای قالب و در سطح آزاد بالایی نشان می دهد؛ که به عنوان دیواره صفحه ای با تنش برشی صفر مدلسازی شده است. مدل REK به همراه مدل “عملیات دیوار تقویت شده” به کار می رود [29،33،34] که امکان اصلاح صحیح لایه مرزی توربولانت را برای لایه‌های مرزی حل‌شده و غیرحل‌شده می‌دهد. بنابراین، فاصله دیوار بدون بعد سلول‌های مجاور دیوار (به اصطلاح مقدار y+) می‌تواند کمتر و بیشتر از 1 باشد، برخلاف روش دیواره کلاسیک، که در آن y+ باید بیشتر از 1 باشد تا اطمینان حاصل شود که سلول مجاور دیواره در لایه مرزی لگاریتمی قرار دارد.

مدل SAS بر پایه معادلات توربولانس k–ω است، در نتیجه هیچ اصلاح دیوار خاصی مستقل از رزولوشن لایه مرزی وجود ندارد. مقادیر y+ به دست آمده در شبیه سازی های عددی بین 3 تا 10 در دیواره های داخلی نیم نازل ریخته گری مداوم و کمتر از 8 در دیواره های قالب است.

برای هر دو نوع شبیه سازی یک فیلد سرعت صفر به عنوان شرط آغازی استفاده می شود و 100 ثانیه محاسبه می شود. گام زمانی برای مدل RKE به میزان 0.01 و 0.001 برای مدل SAS می باشد. گام زمانی اتخاذ شده برای مدل SAS تضمین می کند که سیال به گام زمانی 2.5 برای گذراندن سلول حجمی محدود 5 میلیمتر در یک سرعت جریان عادی به میزان 2 متر بر ثانیه نیاز دارد.

این مورد برای در نظر گرفتن انتشار گرداب هایی که توسط شبکه بدون نفوذ عددی حل می‌شوند، لازم است. در مقابل، اندازه گام زمانی برای مدل RKE می تواند 10 برابر بزرگتر باشد زیرا ویسکوزیته توربولانس بالاتر استفاده شده توسط این مدل از تشکیل خودبخودی گرداب ها حتی در صورت استفاده از گام زمانی کوچک جلوگیری می کند. در نتیجه، سعی محاسباتی برای SAS بسیار بیشتر از مدل RKE است، اما همانطور که در نتایج نشان داده شده تلاطم را می توان با مدل SAS بهتر مدل سازی نمود.

2.2. حباب های گاز

برای شبیه‌سازی حباب‌ها از دیدگاه اویلری برای به دست آوردن توزیع حباب با حل یک معادله انتقال برای فیلد کسر حجمی حباب:

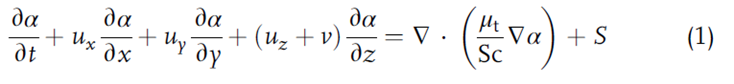
استفاده می‌شود که در آن α کسر حجمی گاز، ux، uy، و uz مولفه‌های سرعت مایع هستند، v سرعت نسبی بین مایع و حباب های گاز، μt ویسکوزیته توربولانس، Sc = 0.7 عدد اشمیت توربولانس و S یک ترم منبع است که برای شرایط مرزی در سلول های شبکه مجاور سطح بالایی جایی که حباب ها از مرز خارج می شوند استفاده می شود. گرانش در جهت z منفی عمل می کند. کسر حجمی گاز در مرز ورودی در نیم نازل ریخته گری مداوم از رابطه دبی حجمی گاز و مایع با فرض سرعت برابر برای هر دو فاز و توزیع هموژن حباب به دست می آید.  

سرعت نهایی بالا آمدن حباب در مایع بدون آشفتگی از فرمول زیر محاسبه می شود:

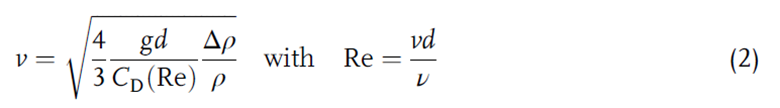
که در آن d قطر حباب، g شتاب گرانشی، Δρ اختلاف چگالی بین مایع و گاز است، ρ چگالی مایع است (برای آب/هوا و آرگون/فولاد نسبت Δρ به ρ تقریبا برابر 1 است)،  C_D (Re) ضریب درگ به عنوان تابعی از عدد رینولدز ذره و ν ویسکوزیته سینماتیکی مایع است. این فرمول یک معادله ضمنی است زیرا v درهر دو سمت معادله موجود است همانطور که Re تابعی از v است. بروکاتو و همکاران [13] اندازه‌گیری‌های ته نشینی ذرات را با اندازه‌ها و چگالی‌های مختلف ذرات در یک مایع انجام دادند، که این بررسی ها نشان می داد که در صورت افزایش توربولانس، سرعت ته‌نشینی کاهش می‌یابد که به دلیل چرخش سیلندر حول محور عمودی آن است. آنها یک اصلاح ضریب درگ را پیشنهاد نمودند که وابسته به مقیاس طول آشفتگی است که در آن توربولانس هموژن در ستاپ آزمایش مفروض است.

نتایج تجربی به خوبی با فرمول کاهش درگ پیشنهادی آنها متناسب است. لین و همکاران [14] شبیه سازی یک مخزن حاوی مایع با حباب های گاز با توربولانس غیرهموژن در حال هم خوردن را بررسی نمودند و نتایج شبیه سازی را با اندازه گیری های مربوط به توزیع حباب مقایسه نمودند.

آنها دریافتند که رابطه بروکاتو تنها در صورتی نتایج نزدیک‌تر به اندازه‌گیری‌های آنها می‌دهد که ضریب عددی معادله کاهش درگ بروکاتو را به طور قابل ملاحظه ای از 8.76×10^-4 به 6.5×10^-6 کاهش دهند.

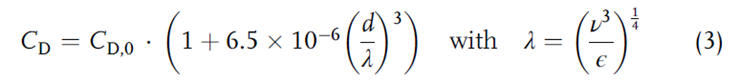
که در آن C_D,0 ضریب درگ بدون هیچ گونه توربولانس، λ مقیاس طول کولموگروف، و ε نرخ پراکندگی توربولانت است. مشاهده اینکه ضریب عددی در معادله (3) باید برای هر موقعیت جریان متناسب سازی شود، نشان می‌دهد که احتمالاً مقادیر جریان یا توربولانس اضافی بر کاهش درگ تأثیر می‌گذارند که در معادله لحاظ نشده است. با این حال، هر مدل توربولانس (به جز شبیه‌سازی‌های عددی مستقیم) تا حدی بر پایه روابط تجربی است و با استفاده از رابطه (3) با ضریب متناسب شده و مقیاس طول لوکال منجر به نتایج خیلی بهتر می‌شود، همانطور که در بخش نتایج نشان داده می شود. با وارد کردن رابطه (3) در رابطه (2) و نادیده گرفتن تغییر ضریب درگ ناشی از تغییر عدد رینولدز ذره در اثر تغییر سرعت حرکت، سرعت بالا آمدن حباب در یک مایع توربولانت مطابق معادله زیر می شود:

که در آن v₀ سرعت بالا آمدن در یک مایع بدون آشفتگی است. ارزیابی عددی معادله دقیق و ساده شده با استفاده از قانون درگ Tomiyama [2] تطابق خوبی از راه حل ساده شده و دقیق را در رنج وسیع تری از سایزهای معمولی حباب و نرخ پراکندگی توربولانت نشان داد (شکل ₂b). برای نتایج شبیه سازی از مقادیرv₀ = 0.23m/s  و  d = 5mm استفاده می شود.

سایز حباب در ابعاد معمول در آزمایش های آب مشاهده می شود (شکل 5) و سرعت بالا آمدن نهایی v₀ برای این سایز با استفاده از نمودار شکل ₂a تعیین می‌شود.

از آنجایی که سرعت نهایی بالا رفتن حباب‌های با این سایز در حد ناچیزی با قطر حباب تغییر می‌کند (شکل ₂a)، انتظار می‌رود که در نظر گرفتن قطرهای مختلف و توزیع سایز تأثیر قابل چشم پوشی داشته باشد و بنابراین سایز حباب ها یکنواخت انتخاب می شود. مقادیر مشابهی برای سایز حباب و سرعت بالا آمدن نیز از آزمایش های صورت گرفته [7] به دست آمده است. در مرحله بعدی پژوهش، مدل عددی برای شبیه سازی وضعیت واقعی مذاب فولاد متناسب سازی می شود و در صورت لزوم، سایزهای مختلف حباب در نظر گرفته می شود. در شبیه‌سازی‌ها با مدل توروبلانس SAS، نرخ پراکندگی با ϵ = 0.09 kω مطابق با تعریف ω محاسبه می شود [29].

در یک جریان مایع دارای حباب زیاد، حباب های گاز مایع را جابجا می کنند. برای مثال، اگر همان سرعت جریان مایع از طریق نیم نازل ریخته گری مداوم در دو (حالت دارای/بدون) کسر حجمی 10 درصد عبور کند، و اگر حباب های گاز به طور همگن در نیم نازل ریخته گری مداوم توزیع شده باشند، سرعت مایع به دلیل جابجایی حجم گاز باید 10 درصد افزایش یابد. این تأثیر در اکثر شبیه‌سازی‌ها با استفاده از محاسبات مسیر ذرات لاگرانژی نادیده گرفته می‌شود (به عنوان مثال، به رفرنس های [18،25] رجوع شود؛ 17 از 31 انتشارات تحلیلی در مورد شبیه‌سازی عددی جریان‌های قالب با حباب‌های گاز، از محاسبات مسیر ذرات لاگرانژی استفاده می‌کنند). در نتایج شبیه سازی ارائه شده، از چگالی مخلوط ثابت استفاده شده و بنابراین، جابجایی حجم گاز نادیده گرفته می شود.

3. بخش تجربی

در کمپانی voestalpine یک مدل آب با مقیاس 1:1 از یک تاندیش و رشته در شکل 4 موجود است. جدول 1 پارامترهای هندسی و فرآیندی را لیست می کند.

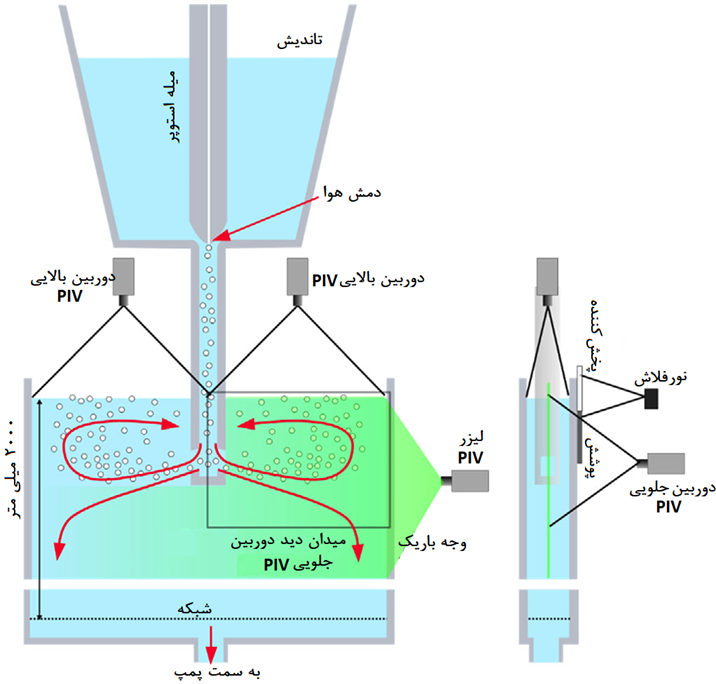
از یک میله درپوش برای کنترل جریان نیم نازل ریخته گری مداوم استفاده شد. برای شبیه سازی دمش آرگون می توان هوا را در نوک میله درپوش تزریق نمود. شکل 5 نمای نزدیک از ناحیه پورت نیم نازل ریخته گری مداوم را نشان می دهد. در این تصویر می‌توان مشاهده نمود که سایز حباب تقریباً یکنواخت و در حدود 5-6 میلی متر است. همانطور که پیش از این ذکر شد، سایز حباب در مدل آب ممکن است با اندازه آن در وضعیت واقعی متفاوت باشد، اما در اینجا فقط وضعیت در مدل آب در شبیه‌سازی عددی و همچنین اعتبارسنجی آن در نظر گرفته می شود.

یک دوربین فیلمبرداری در مقابل مدل آب قالب قرار می گیرد (شکل 4). کلیات توزیع حباب را می توان به صورت کیفی در ویدیو مشاهده کرد. میانگین زیاد زمان نشان دهنده توزیع زمان میانگین است؛ به قسمت نتایج رجوع شود.

دو نوع اندازه گیری سرعت سنجی تصویر ذرات (PIV) انجام شد. مورد اول از روش کلاسیک PIV برای جریان تک فاز (بدون دمش گاز) با دانه بندی ریز، یک صفحه نور لیزری پالسی و یک دوربین PIV برای اندازه‌گیری میدان سرعت دوبعدی در نیمه سمت راست صفحه مرکزی قالب استفاده نمود (شکل 4). روش PIV چند فازی برای نرخ‌های معمولی  دمش گاز غیرقابل اجرا بود زیرا تراکم حباب ها آنقدر زیاد بود که دید دوربین را در صفحه مرکزی مسدود می نمود [24].

برای نوع دوم اندازه گیری PIV، دو دوربین PIV بالاتر از سطح روی قالب قرار می گیرد (شکل 4). حباب‌های روی سطح توسط یک نور فلاش خطی هماهنگ با دوربین‌های PIV آشکار می‌شوند و به عنوان ذرات رهگیری قابل استفاده در الگوریتم PIV برای اندازه‌گیری فیلد جریان در سطح رویی در وضعیت چند فازی استفاده می‌شوند. برای نرخ های معمولی دمش گاز، تراکم حباب و در نتیجه تراکم حباب های رهگیری به اندازه کافی بالا بود و حباب های زیر سطح به خوبی توسط حباب های روی سطح پوشانده شدند.

4. نتایج

در مقایسات زیر بین نتایج اندازه گیری و شبیه سازی، میانگین سازی زمانی برای ردیف های زمانی استفاده می‌شود:

که در آن u_i یک سری زمانی از i = 1 .. n مانند یک جزء سرعت یا شدت تصویر دوربین در یک موقعیت خاص، و ¯u مقدار میانگین زمانی مربوطه در این جایگاه است.

4.1. جریان تک فاز

شکل 6 فیلدهای جریان میانگین- زمان در نیم نازل ریخته گری مداوم در قسمت صفحه مرکزی موازی با وجوه باریک یعنی در ناحیه پورت های خروجی نیم نازل ریخته گری مداوم توسط بردارهای سرعت و همچنین کانتورهای بزرگی سرعت و انرژی جنبشی توربولانت را نشان می‌دهد: برای اندازه‌گیری PIV، انرژی جنبشی توربولانت با ارزیابی دو مولفه نوسان سرعت در صفحه اندازه‌گیری و ضرب آن در 3/2 برای محاسبه مولفه سوم (اندازه‌گیری نشده) عمود بر صفحه اندازه‌گیری برآورد می‌شود[35]:

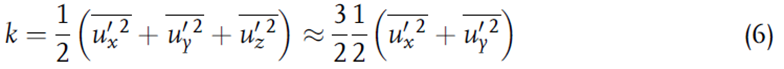
که در آن u ʹ x، u ʹ y، u ʹz مولفه نوسانات سرعت (مقدار واقعی منهای میانگین-زمان) در یک سیستم مختصات لوکال است که برای مشخص کردن آن مختصات x،y با صفحه اندازه گیری تراز و مختصات z عمود بر صفحه اندازه گیری است. برای نتیجه RKE، مقدار لحظه ای انرژی جنبشی توربولانت که توسط مدل آشفتگی جریان محاسبه می شود استفاده می شود. برای مدل SAS، انرژی جنبشی توبولانت از نوسانات حل شده فیلدهای سرعت مشابه با اندازه گیری PIV طبق رابطه (6) محاسبه می شود.

در ناحیه مدنظر، انرژی جنبشی توربولانت محاسبه شده از طریق معادلات مدل SAS تنها توبولانس حل نشده را نشان می دهد و بسیار کمتر از انرژی جنبشی توربولانت محاسبه شده از نوسانات سرعت است. اندازه‌گیری‌های PIV، الگوی جریانی با نوسان شدید نامتقارن را نشان می‌دهد، اما در عین حال یک ساختار گردابی دوگانه متقارن در فیلد جریان میانگین-زمان (شکل 6_a) با انرژی توربولانت زیاد در مراکز گرداب وجود دارد. تنها مدل توبولانس SAS قادر به گرفتن این ساختار جریان است، که به طور قابل توجهی بر جت های آزاد خروجی از پورت های نیم‌نازل و بنابراین ساختار جریان قالب تأثیر می گذارد. بزرگی سرعت رو به پایین در منطقه بالایی ناحیه نمایش داده شده در شبیه سازی SAS کمتر از فیلد جریان PIV اندازه گیری شده است. از طرف دیگر، سرعت ها در مناطق جریان رو به بالا نزدیک دیواره های جانبی نیم نازل ریخته گری مداوم شبیه هم هستند. بزرگی حداکثر انرژی جنبشی توربولانت حاصل از شبیه‌سازی SAS در مقایسه با مقدار اندازه‌گیری شده PIV، تنها حدود 70 درصد است. با توجه به کم بودن توان تعیین انرژی جنبشی توربولانت و با توجه به اینکه این انرژی مدل SAS در ناحیه پایینی نیم نازل ریخته گری مداوم عمدتاً ناشی از نوسانات سرعت جریان ناشی از ناپایداری خودبخودی در این ناحیه است  و تقریبا مستقل از شرایط مرزی توربولانس ورودی واقع در مقطع نیم نازل ریخته گری مداوم است این اختلاف از این لحاظ قابل قبول به نظر می‌رسد.

در شکل 7، فیلد جریان میانگین-زمان در قسمت سمت راست صفحه مرکز قالب عمودی موازی با وجوه عریض مشاهده می شود که با بردارهای سرعت و کانتورهای میزان بزرگی آن مشخص شده است که از اندازه گیری های PIV (تعداد 300 اندازه گیری در 75 ثانیه) و شبیه سازی های عددی استفاده کننده از مدل توربولانس RKE و SAS به دست آمده است. روش PIV دارای رنج سرعت محدودی است و بسته به گام زمانی بین دو تصویر بعدی دوربین، که جابجایی ذرات رهگیری بین دو تصویر را تعیین می کند، برای محاسبه سرعت لوکال استفاده شده است.

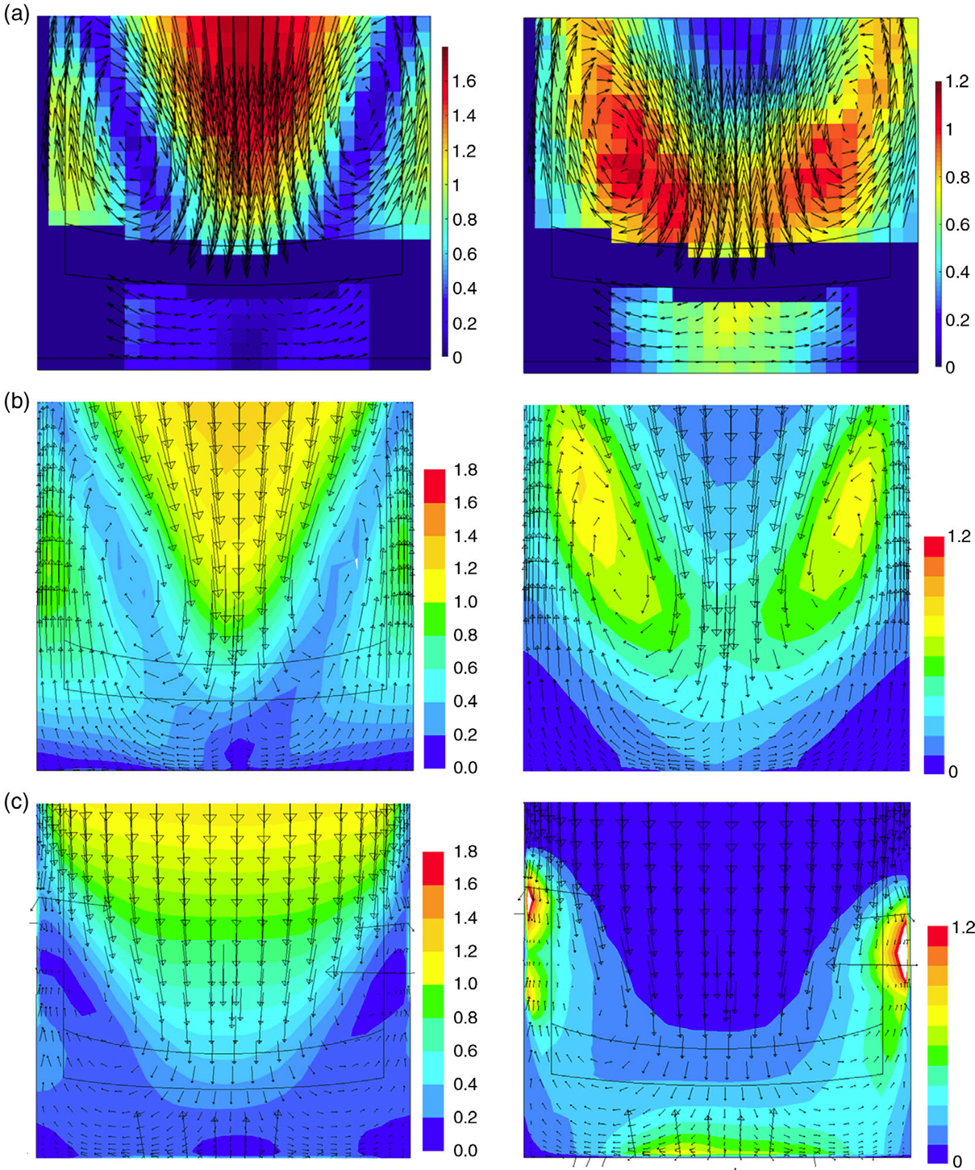
در مناطق با سرعت بالا، جابجایی بسیار زیاد می شود و الگوریتم ارتباط PIV کاربرد خود را از دست می دهد. از سوی دیگر، اگر جابجایی ها در مناطق با سرعت پایین بسیار کاهش یابد، محاسبه سرعت ها نادرست می شود. فاصله زمانی تصویر به گونه ای انتخاب شده است که سرعت قالب به درستی حل شود. بنابراین، سرعت ها در مرکز جت بسیار زیاد است و مقادیر نمایش داده شده مقادیر درونیابی شده از سرعت های پیرامون هستند. در نتیجه، بزرگی سرعت را فقط می توان با شبیه سازی های عددی بیرون از ناحیه مرکزی جت مقایسه نمود.

معیارهای زیر برای مقایسه دقت مدل های عددی در مقایسه با داده های اندازه گیری شده استفاده می شود:

1. یک خط چین که از لبه پورت بالایی شروع می شود، محل مرکز جت آزاد را تعیین می کند که با ماکزیمم سرعت جت از داده های PIV مشخص می شود. این خط همچنین برای نتایج عددی در همان موقعیت هندسی رسم می شود. مرکز جت به دست آمده از فیلد سرعت مدل SAS بسیار نزدیکتر از RKE به این خط است.
2. در نزدیکی ناحیه برخورد جت در وجه باریک، سرعت ها در نتایج RKE بسیار افت می کند، در حالی که نتیجه SAS به داده های اندازه گیری شده نزدیک تر است.
3. حداکثر سرعت در سطح رویی برای همه نتایج تقریباً در نیمه وسطی قالب نمایش داده شده رخ می دهد. درحالی که این مورد در مقادیر اندازه گیری شده و نتیجه SAS برابر 0.3 متر بر ثانیه است؛ مدل RKE ماکزیمم سرعت 0.41 متر بر ثانیه را پیش بینی می کند.

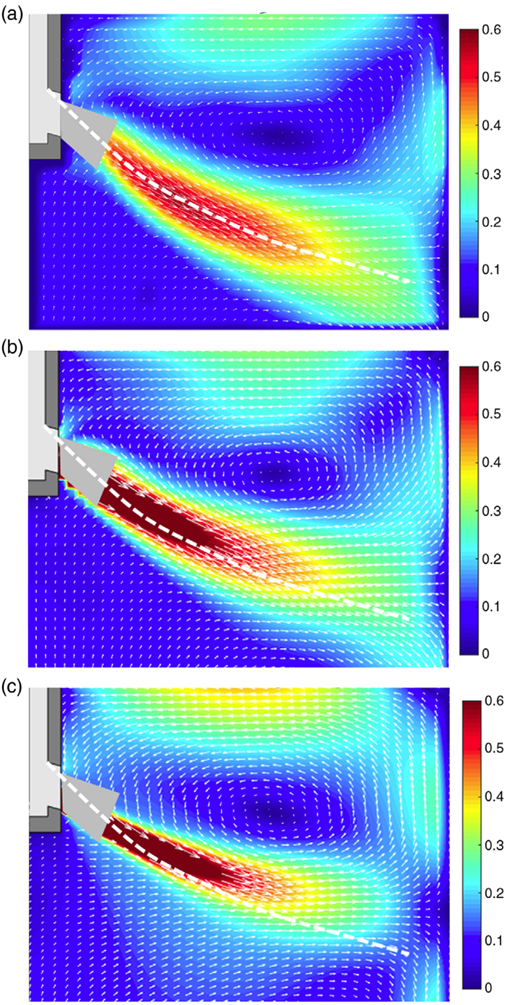
اگرچه که مدل‌های توربولانس ساده مانند RKE به دلیل سعی محاسباتی کمتر بسیار محبوب تر از مدل SAS هستند، اما نتایج به‌دست‌آمده توسط مدل SAS در مقایسه با مدل RKE به اندازه‌گیری PIV بسیار نزدیک‌تر است. بازتولید مناسب مشخصه های جت آزاد و سرعت سطح رویی برای وضعیت چند فازی ضروری است زیرا چگونگی توسعه حباب‌های گاز در قالب را مشخص می کند.

4.2. جریان دو فازی با دمش گاز

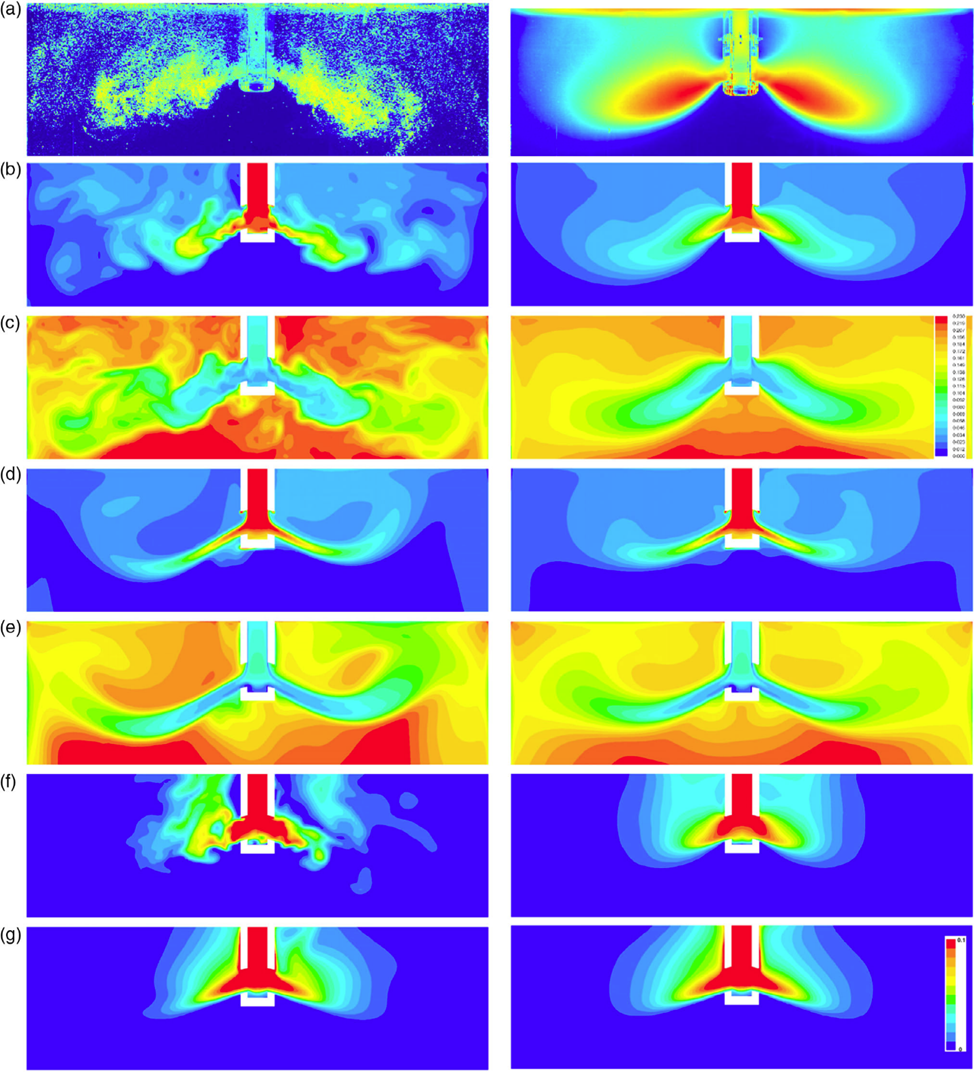
شکل 8 تصاویر لحظه ای از توزیع حباب گاز در مدل آب و از شبیه‌سازی‌های چند فازی انتقالی متناظر با استفاده از مدل آشفتگی RKE و SAS را در هر دو حالت دارای و بدون اصلاح درگ Brucato برای نرخ دمش گاز 40 لیتر در دقیقه نشان می‌دهد که با نرخ دمش آرگون 6.7 لیتر در دقیقه در شرایط استاندارد در مذاب فولاد با انبساط حرارتی گاز با ضریب 6 مطابقت دارد. تصویر دوربین رنگی به تصویری با مقیاس خاکستری تبدیل می شود و سپس با یک نقشه رنگی مانند آنچه برای نتایج عددی استفاده می شود (تاریک = آبی، روشنایی متوسط = سبز، قرمز = حداکثر روشنایی) نمایش داده می شود. در تصویر دوربین، حباب ها به صورت نقاط روشن ظاهر می شوند، در حالی که پس زمینه تیره را می توان در مناطق خالی از حباب مشاهده نمود. در تمام ضخامت قالب عمده نواحی روشن‌ تصویر به‌طور کیفی نشان‌دهنده وجود حباب‌ در این مناطق است. از آنجایی که وضعیت نور یکنواخت نیست و روشنایی تصویر دوربین توسط حباب ها در کل ضخامت قالب (نه تنها در صفحه مرکزی) تعیین می شود، روشنایی تصویر از نظر کمی با کسر حجمی در صفحه مرکزی مرتبط نیست، اما می تواند از نظر کیفی برای دریافت ارتباطی متناظر با توزیع حباب در قالب مقایسه شود. برای نتایج شبیه‌سازی، کسر حجمی حباب گاز در صفحه مرکزی نمایش داده می‌شود. بنابراین، مدل آب و نتایج شبیه‌سازی فقط به صورت کیفی قابل مقایسه هستند. در حالی که مدل SAS توزیع غیرهموژن حباب را همانطور که در مدل آب مشاهده می‌شود حل می‌کند، مدل RKE توزیع گازبسیار یکنواخت تری را تولید می نماید. بدون اصلاح کشیدن Brucato، حباب‌های گاز خیلی سریع در نزدیکی نیم نازل ریخته گری مداوم بالا می‌روند و بنابراین، توزیع حباب در مقایسه با مشاهدات مدل آب، در اطراف نیم نازل ریخته گری مداوم بسیار متمرکز باقی می‌ماند. شکل 8 (c,e) سرعت حباب ناشی از اصلاح درگ Brucato را نشان می دهد. در مناطق با توربولانس بالاتر، سرعت حرکت کاهش می یابد. برای نتایج شبیه‌سازی بدون اصلاح کشیدن Brucato، سرعت حباب نشان داده نمی‌شود زیرا در کل دامین در نظر گرفته شده ثابت است. با توجه به اینکه تصاویر به صورت رندوم از نوسان گرفته می شود، نتایج میانگین-زمانی معنی‌دار تر هستند. بنابراین، یک تصویر دوربین با میانگین زمان طولانی 120 ثانیه با توزیع گاز میانگین زمانی از شبیه‌سازی‌ها، دوباره با مدل RKE و SAS و هر کدام به ترتیب (با و بدون) تغییر درگ Brucato، مقایسه می‌شود. مجددا نتایج شبیه‌سازی عددی با اصلاح درگ Brucato نسبت به نمونه‌های بدون تغییر درگ، به صورت بسیار دقیق‌تری با تصویر دوربین مدل آب مطابقت دارد. شکل 9 نتایج مشابه شکل 8 را برای نرخ های مختلف دمش گاز نشان می دهد (32، 40، 60 و 100 لیتر در دقیقه). تنها نتایج شبیه‌سازی میانگین-زمانی محاسبه‌شده از طریق مدل توربولانس SAS و اصلاح درگ Brucato در مقایسه با تصاویر دوربین میانگین-زمانی گرفته‌شده در مدل آب قالب نشان داده می‌شوند. توزیع گاز با نرخ دمش تغییر می کند، که به نظر می رسد از نظر کیفی به خوبی توسط شبیه سازی ها مشابه سازی شده است. توزیع رنگ چپ-راست کمی نامتقارن در تصاویر دوربین میانگین-زمانی، احتمالا به دلیل وضعیت نامتقارن نور است.

جهت مقایسه کمی ساختارهای جریان اندازه‌گیری و محاسبه‌شده تحت تأثیر دمش گاز، فیلدهای سرعت سطح رویی در نظر گرفته می‌شوند. شکل 10 مقایسه ای از سرعت های جریان میانگین-زمانی اندازه گیری شده و محاسبه شده در سطح رویی قالب برای نرخ های مختلف جریان گاز بین 0 تا 100 لیتر در دقیقه را نمایش می‌دهد. رنگ ها در نمودارهای کانتور مؤلفه سرعت را به موازات وجه پهن قالب هم جهت مرکز قالب نشان می دهند       u_x . signum(-x)، که در آن x محور مختصات موازی با وجه پهن قالب است. شروع با نرخ پایین دمش گاز (ردیف‌های بالا)، اندازه‌گیری‌های PIV (بدون گاز در دسترس نیستند، زیرا هیچ عنصر رهگیری برای روش PIV در این مورد وجود ندارد) یک الگوی جریان دو رولی معمولی با جهت سرعتی به سمت مرکز قالب (نیم نازل ریخته گری مداوم) را نشان می‌دهد. ) (با رنگ آبی تیره مشخص شده است).

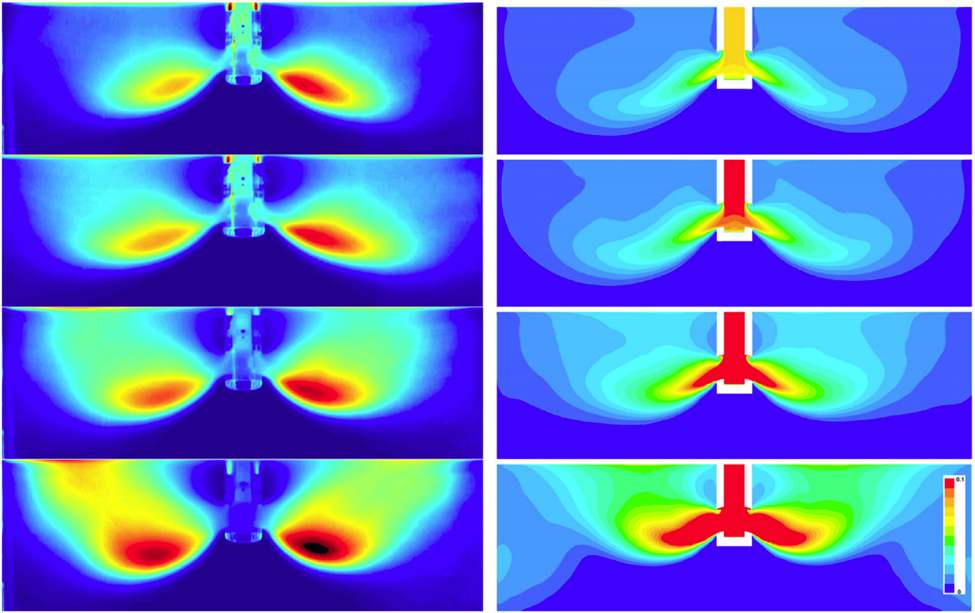
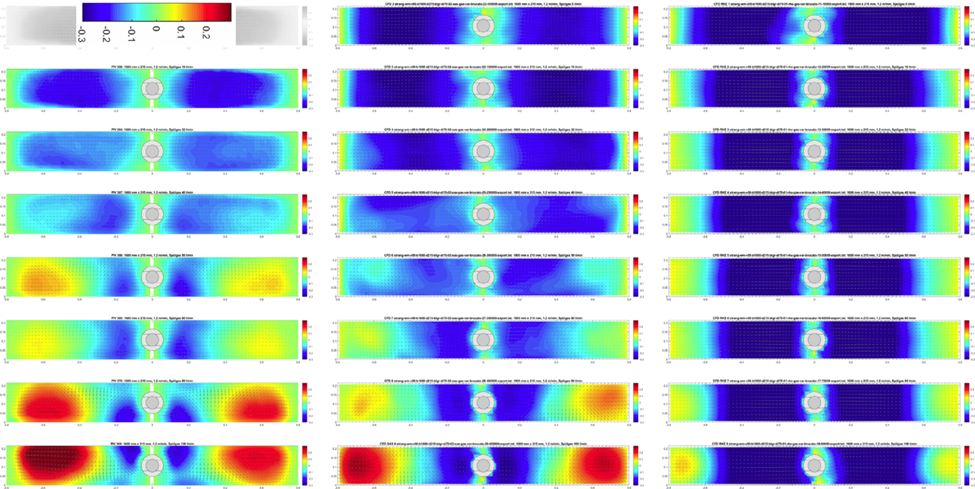
با افزایش نرخ دمش گاز (ردیف های پایین تر)، مقدار سرعت جریان هدایت شده به مرکز قالب کمتر می شود، تا زمانی که الگوی جریان به یک الگوی تک رولی با نواحی بزرگ تغییر می کند که در آن سرعت های جریان از مرکز قالب به سمت وجوه باریک هدایت می شود (با رنگ قرمز نشان داده شده است). در حالی که این انتقال بین الگوی جریان دو رولی و تک رولی به طور کیفی توسط شبیه‌سازی مدل توربولانس SAS (با اصلاح درگ Brucato) شبیه سازی می‌شود، الگوی جریان محاسبه‌شده با مدل توربولانس RKE (و نیز با اصلاح درگ Brucato) به صورت الگوی جریان دو رولی حتی در بالاترین نرخ جریان گاز باقی می ماند. اگرچه تطابق مناسبی بین سرعت سطح رویی قالب بدون دمش گاز بین اندازه‌گیری PIV و شبیه‌سازی SAS وجود دارد، یک تفاوت غیر قابل چشم پوشی برای نرخ‌های دمش گاز هر چند کوچک وجود دارد. با توجه به اندازه‌گیری‌های PIV در شکل 10، حداکثر سرعت سطح رویی برای دمش گاز 16 لیتر در دقیقه فقط 0.24 متر بر ثانیه است، در حالی که حداکثر سرعت محاسبه‌شده توسط توربولانس SAS هنوز 0.3 متر بر ثانیه مشابه وضعیت جریان تک فازی است. به نظر می رسد دمش گاز سرعت سطوح رویی را حتی برای نرخ های پایین گاز کاهش می دهد. برای نرخ‌های جریان گاز بالاتر، نتایج شبیه‌سازی عددی همچنان به الگوی جریان مشابهی می‌رسند و اندازه سرعت (با توجه به نرخ دمش گاز) در مقایسه با نتایج مدل آب تا حدودی تأخیر دارد. یک دلیل می تواند این باشد که حباب ها توربولانس بیشتری را به جریان مایع وارد می کنند، برای مثال، در رفرنس [24] این مورد مشاهده می شود. مدل Sato (رفرنس [20]) در شبیه سازی های بعدی برای در نظر گرفتن این اثر استفاده خواهد شد. در شکل 11 حجم کل گاز در قالب αdV ∫ و انرژی جنبشی جریان dV ½ (ρ u2)∫ به عنوان تابعی از نرخ دمش گاز برای مدل توربولانس RKE و SAS ارائه شده است. متعاقبا انرژی جنبشی فیلد جریان محاسبه‌شده توسط RKE بیشتر از مقدار محاسبه‌شده توسط مدل SAS است، به‌عنوان مثال، سرعت‌های سطح رویی را بیش از حد تخمین می زند. واضح است که اثرات میرایی موجود در جت های آزاد پورت های نیم نازل ریخته گری مداوم با استفاده از مدل SAS بهتر به دست می آید. انتخاب مدل توربولانس همچنین بر رفتار گاز در نرخ های دمش بالاتر تاثیر می گذارد.

5. نتیجه گیری

نتایج مدل آب با شبیه‌سازی‌های جریان عددی نظیر با استفاده از مدل‌های توربولانس RKE و SAS در حالت تک فازی بدون دمش گاز مقایسه می‌شوند. برای نیم نازل ریخته گری مداوم در نظر گرفته شده و هندسه قالب، ویژگی‌های اساسی جریان قالب توربولانت مانند: الگوی جریان جت نیم نازل ریخته گری مداوم و سرعت‌های سطح رویی را می‌توان تنها با مدل توربولانت SAS محاسبه نمود که ساختارهای توربولانس بالاتر را به دست می آورد و حدود ده برابر زمان محاسباتی بیشتری را نسبت به مدل RKE صرف می کند.

برای حالت دوفازی با دمش آرگون، از مدل Brucato استفاده می شود که به وسیله آن می توان سرعت کاهش حباب ها را نیز در نظر گرفت؛ توزیع به دست آمده حباب های گاز در صورتی که مدل Brucato در نظر گرفته نشود با مدل آب تطابق نزدیک تری خواهد داشت (سرعت حرکت حباب ها مستقل از توربولانس است).

برای نرخ های دمش گاز بیشتر، ساختار جریان سطح رویی از دورولی به تک رولی تغییر می کند که می تواند در اندازه گیری های PIV و نتایج SAS مشاهده شود. در مقابل، نتایج RKE نمی‌تواند انتقال از دو رولی به تک رولی را به‌طور رضایت‌بخشی شبیه سازی کند، چون ساختار جریان حتی برای نرخ‌های دمش گاز بسیار زیاد مانند دو رولی باقی می‌ماند. بنابراین به نظر می رسد مدل‌های آشفتگی k-ε از جمله RKE برای شبیه‌سازی جریان قالب تک فازی و دو فازی مناسب نیستند.

در تحقیقات بعدی سعی بر این است که با اندازه‌گیری‌های پیشرفته و مدل‌های شبیه‌سازی عددی، نتایج شبیه‌سازی عددی و اندازه‌گیری‌های مدل آب به هم نزدیک شوند.

اعتبارسنجی باید در تمام گستره پارامتر فرآیند مربوط برای نرخ های دمش گاز، سرعت ریخته‌گری، عمق غوطه‌وری نیم نازل ریخته گری مداوم و ابعاد قالب انجام شود تا توانمندی مدل شبیه‌سازی عددی تضمین شود. تست مستقل شبکه گره دار مشابه رفرنس [36] نیز جهت اطمینان از اینکه گره های استفاده شده به اندازه کافی ریز هستند طراحی شد؛ مشاهده می شود که نتایج حاصل مستقل از اندازه سلول شبکه هستند. نهایتا مدل شبیه‌سازی عددی به حالت فرآیند واقعی (دمش آرگون و فولاد مذاب، شامل اثر انجمادی) منتقل می‌شود.

جهت کسب اطلاعات بیشتر با ما در تماس باشید.