در ماشین های ریخته گری مداوم مخصوصا در سرعت های ریخته گری بالا ممکن است برآمدگی دینامیکی (تغییر در شکل یا بزرگی برآمدگی) رخ دهد و منجر به نوسان ارتفاع مذاب فولاد شده و در پی آن موجب خطرات جدی و یا کاهش کیفیت قابل توجه در فولاد تولیدی شود. رشد مداوم این نوسان ها یا افزایش مداوم سطح قالب نامیده میشود که در نتیجه دو پدیده در کنار یکدیگر منجر به کاهش سرعت ریخته گری می شوند. برای معقول نگه داشتن سرعت ریختهگری و در عین حال کاهش خسارات ناگهانی در فرایند فولاد سازی نیاز مند ابزارهای دقیقی جهت کنترل سطح تیوب مسی هستیم. در این مقاله رویکردی متفاوت در کنترل سطح تیوب مسی ارائه می شود.
این مقاله تغییر استراتژی کنترل در خصوص خروجی را پیشنهاد می دهد که با استفاده از آن می توان به پایداری و ثبات فرآیند دست یافت که این امر منجر به افزایش توان عملیاتی ماشین می شود. همچنین شبیه سازی مدل های تغییرات در حالت های پیچیده نشان دهنده افزایش 20 درصدی تولید می باشد.
1.مروری بر منابع
تقاضا برای فولاد در دهه های گذشته در نتیجه رونق صنعتی پس از جنگ جهانی دوم و در دهه 1990 و همچنین پیشرفت در چین (ناشی از افزایش مصرف گرایی) پس از آغاز هزاره افزایش یافته است و انتظار می رود پس از پایان دهه افزایش بیشتری نیز پیدا کند. دیگر بحران های واقعی نیز ناشی از توسعه در کشورهایی مانند چین و هند است. این دلایل، علاقه به سرعت بالای ریخته گری را به موازات ملاحظات اقتصادی معمول مربوط به کارخانجات فولاد سازی افزایش می دهد. در بسیاری از موارد برای تولید برخی از گریدهای فولاد و سرعت های ریخته گری بالاتر از مقدار معین، پدیده برآمدگی دینامیکی بوجود می آید و همچنین افزایش مداوم سطح قالب می تواند مشکلات قابل توجهی را در این فرایند ایجاد کند. برآمدگی دینامیک نشان دهنده تغییر بزرگی و یا شکل برآمدگی های رشته است که ناشی از تغییر حجم فولاد مذاب موجود در داخل رشته و همچنین نوسانات سطح قالب می باشد، در حالی که افزایش مداوم سطح قالب مترادف با رشد پیوسته این نوسانات است.
برای اطمینان از کیفیت محصول نهایی، تولید مداوم و کارکرد ایمن ماشین، سطح قالب باید تا حد امکان ثابت نگه داشته شود. عملا در صنعت ماشین های ریختهگری مداوم اغلب با سرعتهای پایینتری کار میکنند تا این مشکلات را نداشته باشند، به عبارتی صورت مسئله در این داستان حذف می شود. لذا در بسیاری از موارد اگر سطح قالب تمایل به برآمدگی دینامیک را نشان دهد، سرعت ریختهگری را تا حد زیادی کاهش می دهند. در این نقطه به لزوم استفاده از روش های مناسب کنترل سطح مذاب در تیوب مسی میتوان پی برد.
مطالعات زیادی در سال های اخیر در این خصوص انجام شده است. روشهای توسعهیافته هم در متغیرهای دستی (جریان ورودی فولاد مذاب در قالب، سرعت رشته، تنظیمات نوسان قالب، میزان خنکسازی رشته یا میدانهای الکترومغناطیسی) و هم در اندازهگیریهای مورد استفاده برای کنترل متفاوت است. اندازهگیریهای برآمدگی دینامیکی موارد ذیل را شامل می شوند:
- اندازهگیری مستقیم برآمدگیها
- خمش یا فشار در غلطک ها
- جریان موتورهای رانش یا نیروهای کشاننده
- اندازهگیری سطح قالب
جهت کنترل سطح تیوب مسی تجهیزات مختلفی ساخته شده است. این کنترل کننده ها در فرآیند کاری متفاوت هستند، در بعضی موارد تنها خروجی را نشان می دهد و در بعضی دستگاه ها خروجی منجر به یک عمل کنترلی خودکار نیز میشود.
به عنوان مثال تلاش برای کاهش برآمدگی دینامیکی با روشی که فقط از سطح قالب به عنوان اندازهگیری استفاده میکند و به طور دورهای سرعت ریختهگری را تغییر میدهد توسط Uehara و همکارانش در سال 1998 ارائه شده است. سایر روش های ممکن برای اینکه سطح قالب تا حد ممکن صاف نگه داشته شود (روشهایی که تنها به این اندازه گیری و ثابت نگه داشته شدن سرعت ریخته گری وابسته هستند)، مبتنی بر فناوری های شکل دهی ذیل می باشند:
- حلقه ای با تجهیزات کنترلر زمان افزایش
- تخمین اختلال
- آرام سازی های هارمونیک جداگانه
- کنترل مدل داخلی
- کنترل خروجی منجر به عمل خودکار و کنترل دوره ای
همچنین می توان از اندازه گیری های غیرمستقیم برای کنترل و کاهش ناپایداری سطح تیوب مسی ریخته گری مداوم استفاده نمود. به عنوان مثال در تحقیقات (Bramerdorfer (2002)، Furtmueller (2005) و Gruenbacher (2006))) از جریان های موتور استفاده می شود، همچنین گشتاور رانش غلطک ها در تحقیقات Sugisawa (1993) و نیروی بیرون کشیدن رشته در تحقیقات Tanaka و همکاران کنترل می شود. در تحقیقات Omura (1998)دستگاههای اندازهگیری که بین غلطک ها قرار میگیرند استفاده شد و در تحقیق Kawamoto (1984) فشار تماس غلک ها اندازه گیری و مشخص میشوند. در همه این رویکردها فقط سرعت ریخته گری به گونه ای تغییر داده می شود تا رفتار سطح قالب به ثبات و پایداری برسد. اما در این مقاله رویکردی کاملا متفاوت ارائه شده است. عملیات تنش دار و ناپایدار ماشین نیز مجاز است. این موضوع با ربط دادن نتایج مدرن در تئوری کنترل و نتایج ناشی از تشخیص برآمدگی به یکدیگر حاصل می شود. با استفاده از این رویکرد و یک شبیه ساز کیفیت بالا و تست شده، می توان به افزایش بهره وری در حدود 20 درصد دست یافت. می توان گفت که روش ارائه شده شبیه به رفتار یک اپراتور خوب است. با این حال، روش ما از یک کنترلر اختصاصی برای هر سرعت ریخته گری استفاده می کند. برای تحت کنترل قرار گرفتن این نوسانات کافی است که سرعت ریخته گری کاهش یابد.
2. ریخته گری مداوم فولاد
2.1. فرآیند ریخته گری مداوم
در شکل 1 شماتیک یک سیستم ریخته گری مداوم نشان داده شده است. در این فرایند فولاد مذاب از پاتیل به تاندیش ریخته می شود.
از تاندیش تا قالب مسی آبگرد، فولاد مذاب از میان یک سیستم تخلیه (معمولا سیستم استوپر فرمانگیر یا یک سیستم اسلاید گیت، یک لوله و سپس نازل غوطه ور یا همان نیم نازل) عبور می کند.
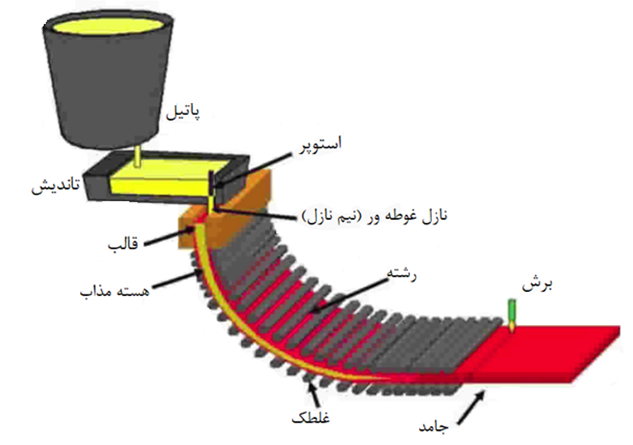
سپس رشته تولید شده به بیرون از قالب مسی منتقل می شود و توسط غلطک ها به سمت پایین سیستم انتقال پیدا می کند، در حالی که خنک کاری بدون هیچ گونه وقفه ای در فرآیند جهت انجماد در حال انجام است و در نهایت می توان رشته را به شکل اسلب، شمش، بلوم یا هر مقطعی برش داده و از سیستم خارج نمود.
2.2 ساختار مدل
فهرستی از اجزای اصلی یک سیستم ریختهگری مداوم و تأثیرات مؤثر بر کنترل سطح تیوب مسی را میتوان در تحقیقات Furtmueller (2007) و Passenbrunner (2009) یافت.
شکل 2 مدل پایه را نشان می دهد که با ترکیب این اجزا و نادیده گرفتن تاثیر ارتفاع سطح پر شدن تاندیش، هندسه سیستم تخلیه و سطح قالب به دست آمده است. با در نظر گرفتن این مفروضات، هر ترکیبی از سیستم فرمان گیر و نازل غوطهور (نیم نازل) و همچنین سنسور را میتوان به عنوان یک فیلتر پایینگذر درجه اول مدلسازی کرد. فیدبک خروجی داخلی از طریق رشته توسط سیستم های دینامیک و تاخیرهای زمانی دریافت می شود. هر یک از 14 جفت غلطک در بخش قالب برآمده به یک سیستم مرتبه سوم بدون تأخیر زمانی نیاز دارد.
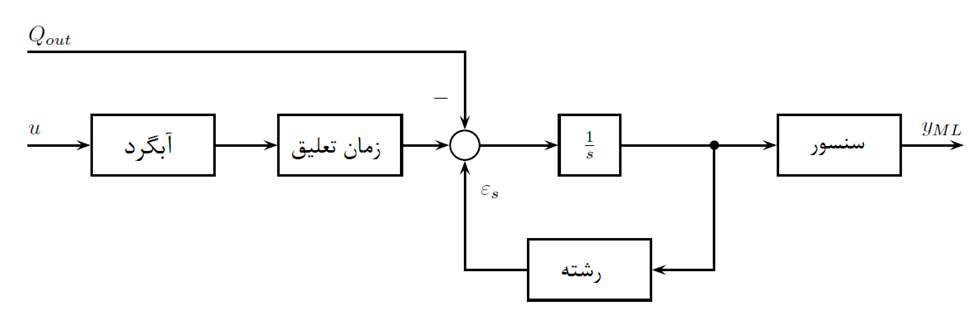
ورودی کنترل، در سیستم مورد بررسی، موقعیت استوپر (با برچسب u)، Qout دبی خروجی قالب و yML سطح قالب اندازه گیری شده را توصیف می کند.
سیگنال میانگین جریان رانش موتورهای الکتریکی:
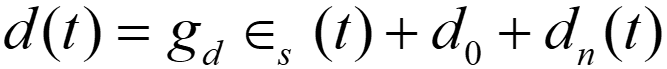
که توان غلطک های آبگرد را تامین می کند و شاخص برآمدگی دینامیک را ارائه می دهد. dn(t) یک اختلال غیرقابل پیش بینی کوچک را توصیف می کند، d0 تغییر آهسته انحراف است، که می تواند ثابت فرض شود. gd ثابت فرض می شود و می تواند برای یک ماشین معین محاسبه شود، s(t)∋ سیگنال برآمدگی دینامیک است.
2.3. مدل برآمدگی
دلیل برآمدگی را می توان در فشار فرواستاتیک متغیر فولاد مذاب در داخل رشته بین حدود 100 غلطک آبگرد یافت. برخی از آنها به طور فعال رشته را به حرکت در می آورند. جریان اضافی QBulg (t) به قالب را می توان به معادله زیر تقسیم کرد:
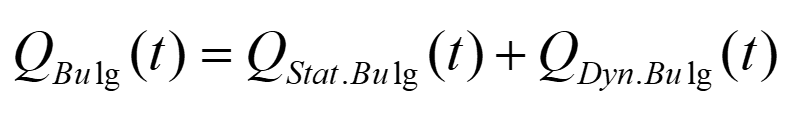
که در آن QStat.Bulg (t) تقریبا ثابت برآمدگی استاتیک را توصیف می کند که به آرامی تغییر می کند و عمدتا به دلیل برآمدگی دینامیک به سرعت خنک کننده، گرید فولاد و جریان QDyn.Bulg(t) به معادله زیر بستگی دارد.
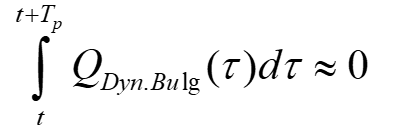
Tp طول دوره است که عمدتا با فاصله بین غلطک ها و سرعت ریخته گری تعیین می شود.
مشکلات برآمدگی دینامیک و افزایش سطح قالب در برخی از ماشین ها بیشتر از سایرین رخ می دهد که به مواد در حال تولید و چیدمان هندسی غلطک های پینچ رشته بستگی دارد. اگر زمانی که سطح قالب تمایل به برآمدگی دینامیک را نشان میدهد، سرعت ریختهگری کاهش نیابد، افزایش سطح قالب میتواند بیشتر شود و باعث بیرون ریزی قالب یا ترک خوردن در پوسته رشته شود.
2.4. شبیه ساز
شبیهساز موجود قبلا بر اساس دادههای اندازهگیری ثبت شده در یک ماشین ریختهگری مداوم واقعی برای طراحی موفقیتآمیز شماتیکی جبران برآمدگی پیشبینی شده استفاده شده است. علاوه بر بالا آمدگی دینامیک و افزایش مداوم سطح قالب، انواع اختلالات احتمالی را می توان در شبیه ساز در نظر گرفت. این اثرات در فرآیند کنترل سطح تیوب مسی را می توان به طور کلی به پنج دسته تقسیم کرد:
- اختلالات بر روی سیستم فرمانبر استوپر
- اختلالات در تغییر دبی جریان ورودی
- اختلالات روی سطح فولاد مذاب در قالب
- نوسانات قالب
- اختلالات ناشی از رشته
مقایسه بین داده های اندازه گیری شده و شبیه ساز در شکل 3 نشان داده شده است. سطح قالب فقط انحرافات جزئی را نشان می دهد و منعکس کننده کیفیت شبیه ساز استفاده شده در پی آن است.
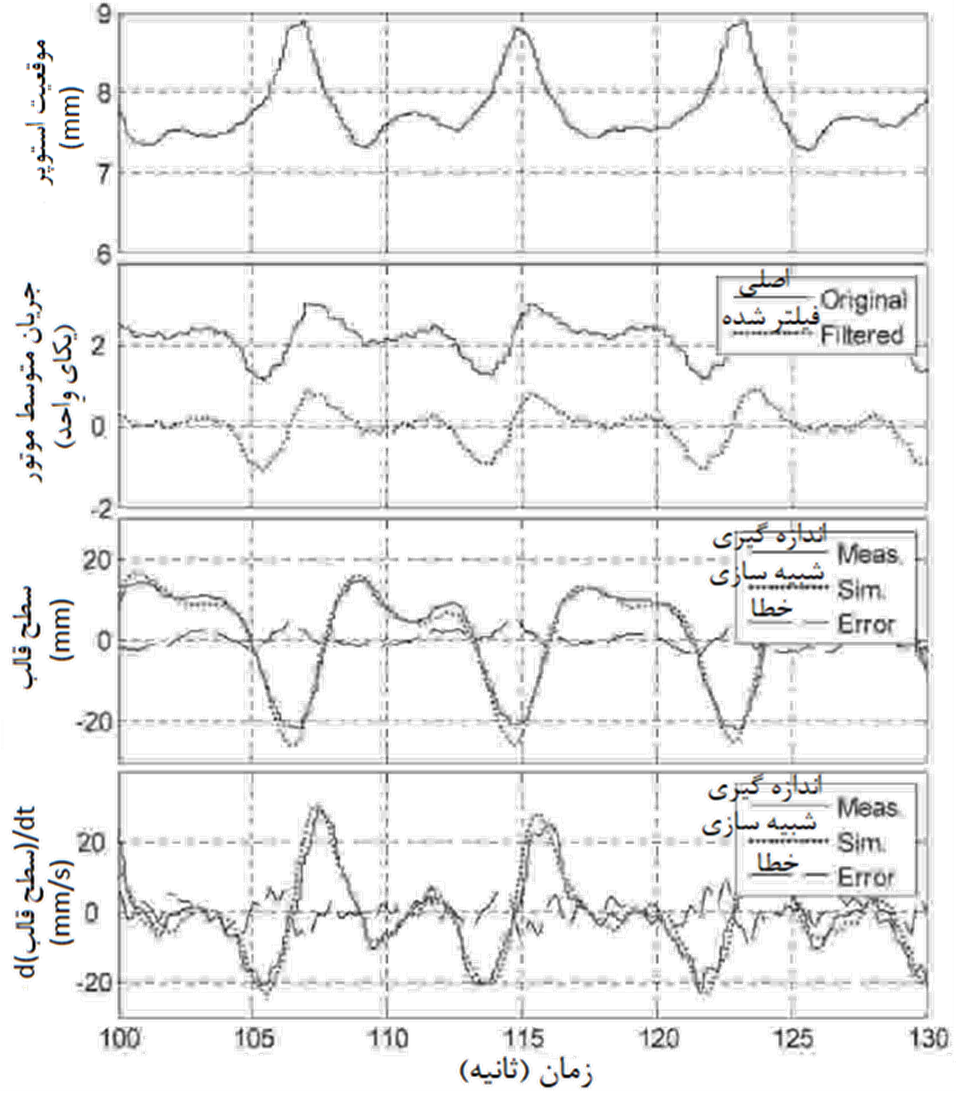
3. مبانی کنترل سوئیچینگ
یک احتمال برای دستیابی به یک استراتژی تعویض (سوئیچینگ) با رویکرد میانگین زمان تعلیق ارائه شده است. در این مورد قانون کنترل سوئیچینگ فقط وابسته به زمان است. یکی از الزامات برنامه تکرارپذیری فرآیندی است که تنها تا حدی در صورت برآمدگی دینامیک تضمین می شود. با این حال امکان تخمین حداکثر سرعت متوسط ریخته گری را فراهم می کند.
امکانی دیگر با روش کنترل خروجی دینامیک ارائه می شود، یک سیستم سوئیچ شده خطی که از شرایط اولیه صفر تکامل می یابد و توسط معادلات زیر ارائه می شود:
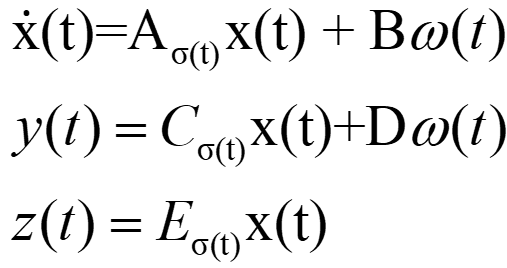
بردارهای زیر پارامتر های حالت، اختلال بیرونی (exogenous)، خروجی اندازه گیری شده و خروجی کنترل شده را مشخص می کنند:
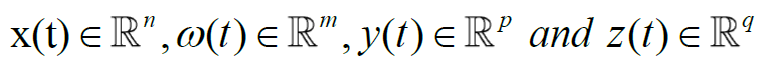
تابع (τ) σ نشان دهنده سیگنال سوئیچینگ است:
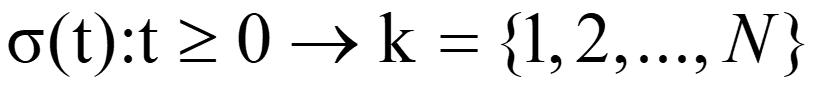
اکنون هدف یافتن قانون کنترل خروجی است که صرفاً به اطلاعات موجود بستگی دارد.
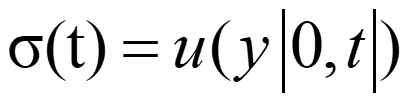
که در آن مسیر زیر با مبدا x=0 به یک نقطه تعادل مجانبی پایدار تبدیل می شود:
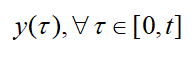
از آنجایی که تابع u(0) تابعی از y است، واضح است که یک فیلتر با y (t) به عنوان ورودی به صورت زیر:
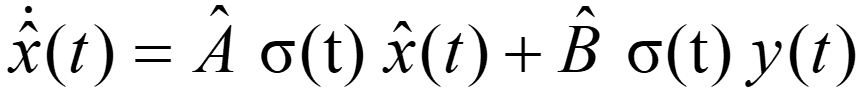
و شرایط اولیه صفر تعریف شود. با ترکیب سیستم خطی سوئیچ شده و این فیلتر معادلات زیر به دست می آید:
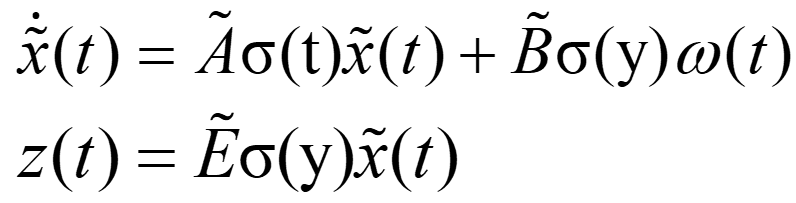
با در نظر گرفتن:
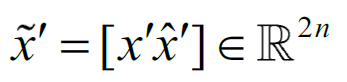
و همچنین:
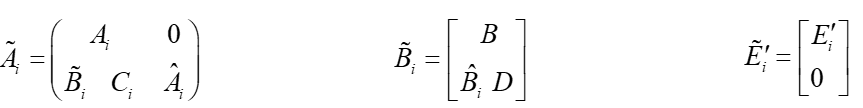
راه حل مساله برای تعیین ماتریس های Ai و Bi برای هر i عضو K و یک قانون سوئیچینگ، همچون سیستم خطی سوئیچ شده گسترش یافته پایدار مجانبی است.
برای گنجاندن قانون سوئیچینگ تنها وابسته به اطلاعات موجود در تحقیقات Geromel و همکاران (2008) جست و جو برای راه حل نامساوی های Lyapunov-Metzler با ساختار تعیین شده ماتریس های تشریحی مثبت محدود شده است:

به طوریکه X نیز یک ماتریس تشریحی مثبت است. به دلیل عبارت:
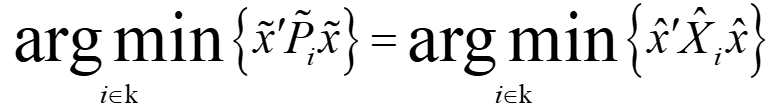
نیاز به یک قانون پایدارساز ترم زیر:
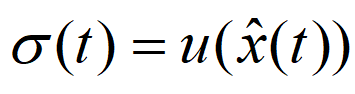
مطابق معادله زیر داریم.

اگر ماتریس دوم Metzler موجود باشد، ماتریس های تشریحی مثبت و ماتریس های فیلتری و به ازای هر i عضو K که نامساوی Lyapunov-Metzler را برآورده کند:
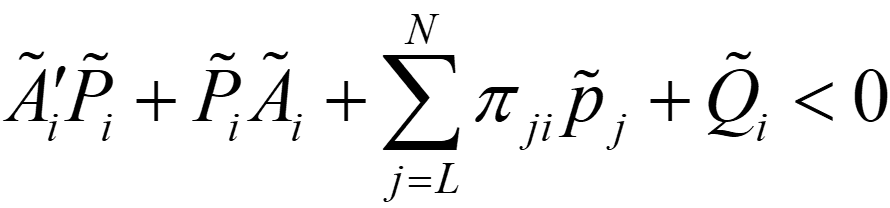
شرایط لازم بر اساس نامساوی های ماتریس برای وجود ماتریس های فیلتر و ، مجددا در تحقیات Geromel (2008) ارائه شده است.
4. مدل ساده شده فرآیند
از آنجایی که شبیه ساز بسیار پیچیده است و نامساوی های ماتریس خطی باید برای تعیین قانون سوئیچینگ و ماتریس های فیلتر حل شود، لازم است یک مدل ساده شده برای طرح کنترل محاسبه شود.
همانطور که نشان داده شده است، ایجاد مدل های ساده شده برای حلقه بسته متشکل از فرآیند و یک کنترل کننده اختصاص داده شده برای هر ریخته گری نسبت به در نظر گرفتن فرآیند تنها مناسب تر است.
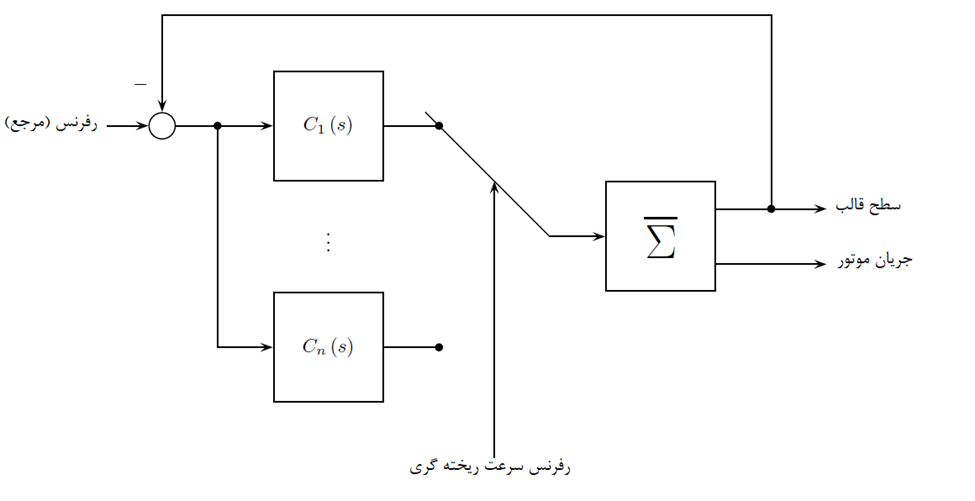
بلوک Σ نشان دهنده مدل فرآیند است (در شکل 2 ملاحظه شود). حلقه از طریق سطح قالب اندازه گیری شده yML و یک کنترلر PID با مشخصه Ci (s) که i =1,…,n برای هر سرعت ریخته گری بسته می شود. این حلقه بسته متعاقباً نامگذاری می شود (در شکل 6 ملاحظه شود). خروجی مدل ساده شده همان رفتار ماشین واقعی و شبیه ساز را نشان می دهد.
در حالی که برای سرعت کم و متوسط ریختهگری، رفتار حلقه بسته پایدار است، برای سرعت های بالا این فرضیه درست نیست. مروری بر سرعت های ریخته گری استفاده شده در جدول 1 آورده شده است.

در شکل 5 میانگین سیگنال جریان موتور ثبت شده برای حلقه بسته شامل مدل فرآیند و یک کنترل کننده PID برای سرعت ریخته گری 1.0 متر بر دقیقه و 30 دقیقه نشان داده شده است. می توان دید که نوسان یک موج سینوسی خالص نیست، بلکه از چندین جزء فرکانسی تشکیل شده است.
یک جایگزین برای استفاده مستقیم از این سیگنال برای جلوگیری از تعویض مکرر بین سرعت های ریخته گری مختلف، توسعه مدل هایی است:
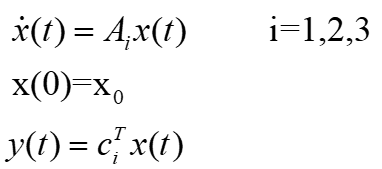
که فرض می شود ساختار زیر را دارند:

برای این منظور سیگنال جریان متوسط موتور توسط یک پایین گذر، تبدیل (rectifiy) و فیلتر می شود. برای اطلاعات بیشتر و جزئیات بیشتر در مورد تعیین پارامترهای αi, 1, αi, 2, ωi, ci, 1و ci, 1 به Passenbrunner (2009) مراجعه نمایید.
5. کنترل خروجی
اطلاعات دریافت شده از وضعیت سطح مذاب به عنوان خروجی در اختیار کنترلر قرار میگیرد. به کارگیری قانون کنترل خروجی در گام اول دید بیشتری را در مورد فرآیند سوئیچینگ می دهد و امکان تشخیص و رفع خطا را فراهم می کند.
5.1. کنترل خروجی
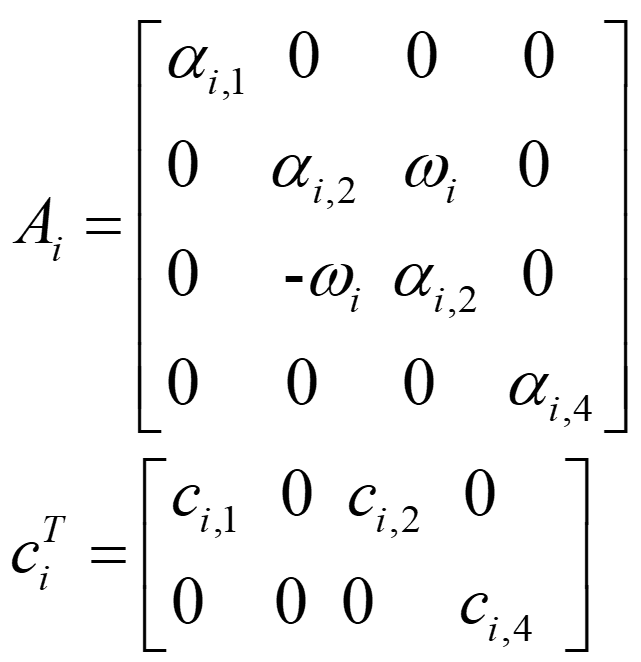
هدف از کنترل خروجی ایجاد یک قانون سوئیچینگ مطابق معادله پایین است که راه حل تعادل x = 0 را به طور مجانبی پایدار می سازد:
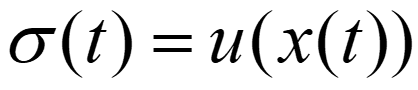
جزئیات بیشتر در مورد پایدارسازی سیستم های خطی سوئیچ شده زمان-پیوسته را می توان در تحقیقات Geromel و Colaneri (2006) یافت.

در مورد مدل ساده شده توسعهیافته، این الگوریتم فقط سعی میکند تا به صورت مجانبی شرایط را در سریعترین زمان ممکن پایدار سازد. سرعت ریخته گری در نظر گرفته نمی شود. بنابراین برای به حداکثر رساندن میانگین سرعت ریختهگری، حالت دیگری مستقل از همه حالتهای دیگر اضافه میشود:
اگر حالت اول یا دوم در حال استفاده باشد مقدار حالت x4 به طور پیوسته افزایش می یابد و با اعمال حالت سوم در حال کاهش است. حالت معرفی شده x4 کاری جز جبران کردن استفاده از کمترین و یا متوسط سرعت ریخته گری انجام نمی دهد.
به دلیل تضاد اهداف کاری بین حالت های x1 و x4 و بنابراین تغییر مکرر سرعت ریخته گری، معرفی تغییرات پسماند مشابه کنترل کننده حالت لغزشی مفید است. این انتخاب نشان دهنده تعادل بین سرعت ریخته گری قابل دستیابی و افت کیفیت محصول نهایی است.
5.2. کنترل خروجی دینامیک
گسترش روش ارائه شده در بالا با استفاده از فیلترهایی مورد نیاز است، زیرا فقط سیگنال جریان متوسط موتور اندازه گیری شده هم در ماشین واقعی و هم در شبیه ساز موجود است. پارامترها و تنظیمات به دست آمده در زیربخش قبلی را می توان مستقیماً به روش کنترل خروجی دینامیک منتقل کرد.
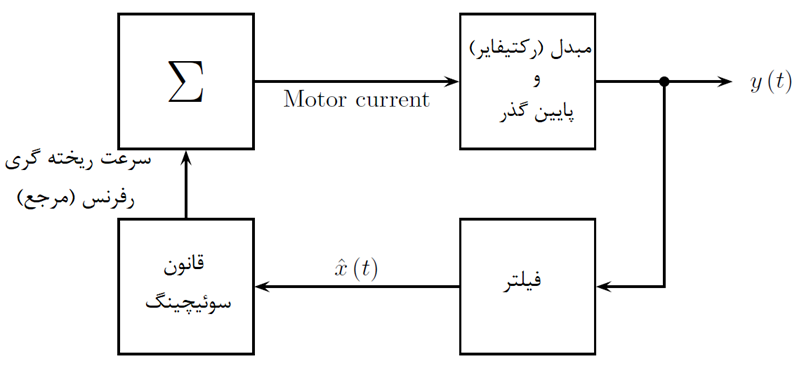
با استفاده از این روش سیگنال خروجی y (t) در مورد در نظر گرفته شده توسط نویسنده، سیگنال جریان متوسط موتور تبدیل شده و فیلتر شده پایین گذر از طریق فیلتر سوئیچ جدید اعمال شده برگشت داده می شود. اصل روش استفاده شده در شکل 6 نشان داده شده است.
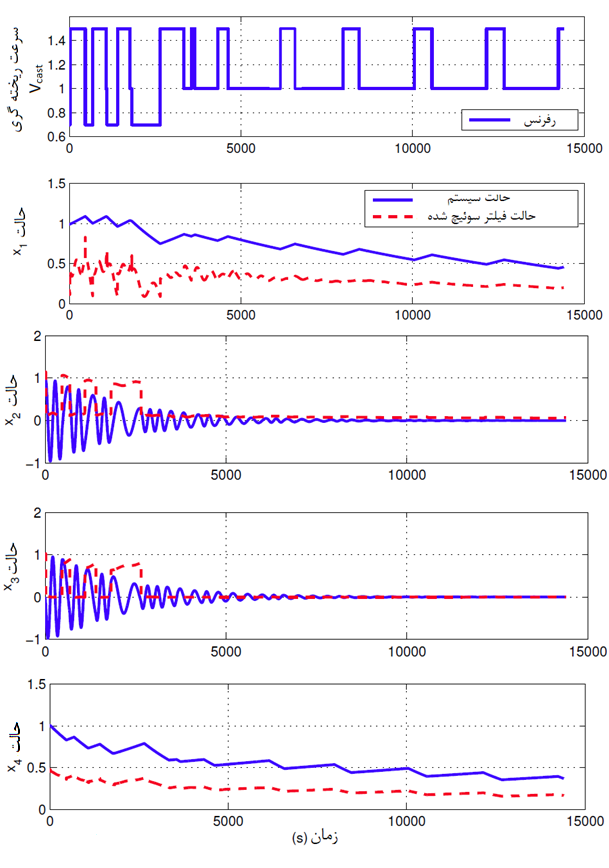
در نمودار اول شکل 7، رفرنس سرعت ریخته گری دیده می شود، در حالی که چهار مورد دیگر حالت های x1 تا x4 سیستم را به صورت خطوط توپر و حالت های ˆx1 تا ˆx4 فیلتر سوئیچ شده را به صورت خط چین نشان می دهند.
عملکرد مورد نظر با در نظر گرفتن موارد زیر می تواند تحقق یابد:
- کمترین سرعت ریخته گری تنها زمانی اعمال می شود که سطح قالب نوسانات زیادی را نشان می دهد. بنابراین این حالت باید برای موقعیت های شدید و اضطراری در نظر گرفته شود.
- زمان عملکرد یک حالت معین از چند صد تا چند هزار ثانیه افزایش می یابد
شکل 7 نشان می دهد که تمام حالات سیستم و حالت های فیلتر سوئیچ شده وقتی زمان به سمت بینهایت می رود به سمت صفر میل می کند. انحراف های از سیگنال صفر به صورت نوسان باقی می ماند.
رفرنس و مقدار جریان سرعت ریختهگری، سیگنال متوسط جریان موتور و سطح قالب نشانداده شده در شکل 8 در شبیهساز غیرخطی دارای همان تنظیمات قبلی ضبط شده است و مباحثی اساسی را در این زمینه ارائه میکند. میزان تأخیر نشاندهنده زمان مورد نیاز یک ذره فولاد برای حرکت در امتداد فاصله از سطح قالب تا بخش برآمده برجسته بر روی شبیه ساز است که با تقسیم رفرنس سرعت ریختهگری بر این گستره محاسبه میشود. به همین ترتیب زمان مورد نیاز این ذره برای حرکت از یک جفت غلطک به جفت غلطک بعدی با تقسیم بر فاصله بین دو جفت غلطک تعیین می شود. اگرچه فیلتر کردن این رفرنس در مسیر فیدبک خروجی داخلی از طریق رشته صورت می گیرد، اما پیکها در سیگنال جریان متوسط موتور را میتوان در زمان سوئیچینگ وارد شده به اجرای مسیر فیدبک خروجی داخلی با سیستمهای دینامیکی و تاخیرهای زمانی در نرم افزار متلب و یا Simulink دیتکت نمود.
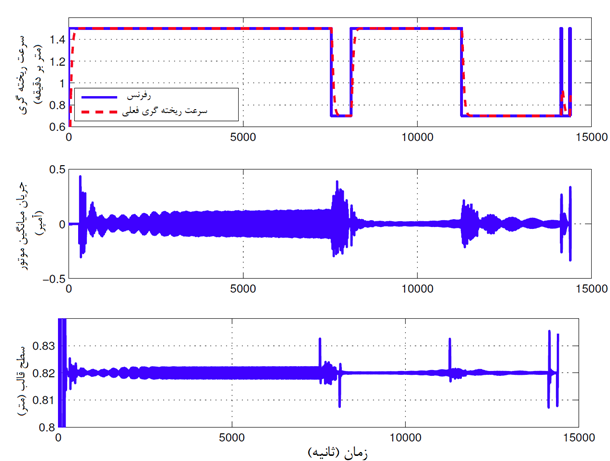
با این حال، همانطور که توسط اندازه گیری ها نشان داده شده است، این اوج قدرت در ماشین واقعی رخ نمی دهد. در عوض، سرعت رشته کم و بیش به آرامی به میزان رفرنس تنظیم می شود. تخمینی از این مورد را می توان بر اساس توان غلطک هایی که رشته را می رانند، جرم رشته و اصل مونتوم خطی تعیین کرد.
- پیک های قابل توجهی را می توان چند صد ثانیه پس از شروع شبیه سازی مشاهده کرد. این پیک ها از راه اندازی سیستم های دینامیک و تاخیرهای زمانی ناشی می شوند.
- هنگامی که از بالاترین سرعت ریخته گری استفاده می شود، همانطور که از توسعه مدل ساده شده به خوبی فهمیده شد در همان ابتدا اندازه دامنه جریان متوسط موتور شروع به رشد می کند؛ با این حال، تنها رشد کند را می توان تشخیص داد و همچنین دامنه نوسان انباشته پس از رسیدن به عددی خاص کاهش می یابد.
6. نتیجه گیری و چشم انداز
روش ارائه شده در این مقاله به ما این امکان را ارائه می دهد تا یک ماشین ریخته گری مداوم را به صورت امن و با سرعت ریخته گری که رفتار پایدار برای آن در شرایط عادی تنها با یک کنترل کننده امکان پذیر نیست، راه اندازی کنیم. در حالی که برای سرعت ریخته گری 1.1 متر بر دقیه، ما توانایی تثبیت رفتار شبیه ساز موجود با یک کنترلر PID را نداریم، با استراتژی های کنترل سوئیچینگ و یک کنترل کننده ساده و اختصاص داده شده برای هر سرعت ریخته گری، امکان دستیابی به مقادیر بالاتر وجود دارد (به جدول 1 رجوع کنید).
افزایش در سرعت متوسط ریخته گری، هم با استفاده از مدل های ساده شده توسعه یافته و هم در شبیه ساز غیرخطی دارای عملکرد متناوب، در عملکرد ناپایدار ماشین، حاصل می شود. مزیتی افزوده نیز نشأت گرفته از در دسترس بودن اندازه های لازم است. هیچ هزینه اضافی جهت نصب دستگاه های اندازه گیری بیشتر تحمیل نمی شود.
روش توسعهیافته فرصتهایی را برای بهبود و ارتقا ایجاد می کند. برای مثال، تطبیق فاکتور دستیابی به پسماند الزامات کیفیت، یکی از این نکات را نشان میدهد. توسعه امکان پذیر دیگر ترکیبی از کنترل خروجی دینامیک با زمان میانگین تعلیق است. به عنوان مثال می توان یک طول مدت سیکل ثابت را انتخاب نمود، در حالی که نسبت بین حالت های مختلف بسته به نوسانات دوره ای سطح قالب تنظیم می شود. با تعداد محدودی از عملیات های سوئیچینگ می توان فرآیند ریخته گری مداوم را پایدار نمود.
در بسیاری از موارد، تغییرات ناگهانی در مواردی همچون تزریق گاز آرگون از عوارضی مانند گرفتگی نازل ها جلوگیری می کند. این روش اغلب عاملی تاثیرگذار جهت کنترل برآمدگی دینامیک است. همچنین می توان با گسترش روش پیشنهادی و کاهش اولیه سرعت ریخته گری از این امر جلوگیری نمود.
برای کسب اطلاعات بیشتر با ما در تماس باشید.