مقاله بیرینگ – تئوری صلبیت بیرینگ

چکیده (مقاله تئوری صلبیت بیرینگ):

تئوری صلبیت اخیرا به عنوان یک ابزار موثر در فیلد کنترل سیستم های چندعاملی پیشرفته ظاهر شده است. تشکیلات روبات های چندتایی و پهبادها که با سنسور شناسایی، توانایی‌های ارتباط و جابجایی مشخصه یابی می‌شوند از جمله این سیستم‌های چندعاملی هستند. در این مقاله خواص صلبیت قاب‌های تعبیه شده در فضای یوکلین Special Euclidean space – SE3 که هر عامل 6 بازو (DoF) است شرح داده می‌شود. در این سناریو، فرض می‌شود که تجهیزات قادر به جمع آوری اندازه گیری‌های بیرینگ با توجه به همسایه های آن است. هدف شناسایی تغییر شکل‌های قاب به قصد نگه‌داری صلب این اندازه‌ها است. دراین مقاله خواص صلبیت به صورت ریاضیاتی فرموله شده و با سایر مطالعات در این زمینه تفاوت کاری دارد. تفاوت به این دلیل است که در این مقاله محاسبات در فضای سه بعدی با دوران‌های چندگانه صورت می‌گیرد. در واقع تمرکز بر صلبیت SE3 بینهایت کوچک است که برای شرایط این نوع مسائل ضروری است.

مقدمه (مقاله تئوری صلبیت بیرینگ):

لغت صلبیت عموما متوجه تئوری ترکیبی مشخصه یابی سفتی سازه‌های تشکیل‌شده از بدنه متصل به لولا و اتصالات می‌باشد. به طور خاص، منظور تغییر وضعیت مکانی بدنه جسم در عین حفظ موقعیت نسبی قسمتهایی خاص از آن است.

به همین دلیل، تئوری صلبیت شامل ارزیابی خواص چندین سیستم ریشه گرفته از مواردی همچون: مکانیک و سازه های ساختمانی، ترکیبات بیولوژیکی و مصنوعی، مواد صنعتی می شود؛ اخیرا نیز این واژه در زمینه سیستم های چند عاملی و تعاملی موقعیت خاصی یافته است. اساسا چارچوب صلبیت برای کاربردهای: کنترل تحرک روبات‌های متحرک سنسورهای همکاری موقعیت‌یابی، جست‌و‌جو، نقشه یابی و رهگیری هدف مورد استفاده قرار می‌گیرد. عموما این مورد به خاصیت معماری مهمی باز می‌گردد. این خاصیت شامل تعدادی سیستم چندعاملی است که در آن یک چارچوب مرجع اینرسی در دسترس نیست اما توسط  تشخیص سنسوری، توانایی ارتباطی و حرکتی مشخصه یابی می شود.

بر طبق اندازه گیری های سنسوری در دسترس، خواص صلبیت به فریم ورکی مربوط می‌شود که با فاصله بین عاملی و نگه داری جهت سروکار دارد. هنگامی که عامل ها فقط قادر به جمع آوری اطلاعات بازه باشند، قیدهای فاصله را می توان برای حفظ ویژگی های صلبیت فاصله اعمال کرد. از طرف دیگر خواص صلبیت بیرینگ/موازی توسط قیدهای جهت تعریف شده بر اندازه گیری های بیرینگ/زاویه تعیین می‌شوند.

مفاهیم اصلی در مورد صلبیت فاصله در مراجع 5 تا 8 نشان داده شده است: این تحقیقات توضیح می‌دهند که چگونه قیدهای فاصله برای یک فریم ورک را می‌توان در یک ماتریس یکتا خلاصه کرد که رتبه آن (تعداد سطر و ستون ماتریس) ویژگی‌های صلبیت بینهایت کوچک سیستم را تعیین می‌کند و شرایط لازم و کافی را فراهم می‌کند. در چنین زمینه‌ای، یک فریم ورک به طور کلی با استفاده از مدل میله و اتصال نشان داده می‌شود که در آن عوامل به‌عنوان نقاطی نشان داده می‌شوند که توسط میله‌هایی به هم متصل شده‌اند که طول آن‌ها قیدهای فاصله بین عاملی را اعمال می‌کنند. ویژگی‌های صلبیت بینهایت کوچک مربوط به حرکات حفظ فاصله فریم ورک است، که بنابراین فقط از انتقالات-دورانی کل سیستم متشکل از یک بدنه صلب تشکیل شده است. تا آنجا که به صلبیت یاتاقان در مجموعه اعداد حقیقی دوبعدی (R²) (یا صلبیت موازی) مربوط می‌شود، با تعریف قیدهای نرمال بر جهت‌های عوامل همسایه، یعنی لبه‌های نمودار سنجش/ارتباط فریم ورک، همانطور که در رفرنس 8 توضیح داده شد، تعیین می‌شود.[8]–[13]. این قیدها مستلزم حفظ زوایای تشکیل شده بین جفت عامل ها و خطوطی است که به آنها می پیوندند، یعنی بیرینگ های بین عاملی. در نتیجه، حرکات بی نهایت کوچک جمعی مجاز فقط شامل انتقالات سراسری و مقیاس بندی یکنواخت کل مجموعه موقعیت ها در فریم ورک است.

در نتیجه، حرکات بی نهایت کوچک جمعی مجاز فقط شامل انتقالات سراسری و مقیاس بندی یکنواخت کل مجموعه موقعیت ها در فریم ورک است. همان حرکات بی نهایت کوچک، فریم ورک های بسیارکوچک صلب بیرینگ را در مجموعه اعداد حقیقی با d بعد مشخص می‌کند. به طوریکه اندازه گیری بیرینگ بین عوامل i و j با زاویه بین محور x سیستم مختصات محلی گره i و پاره خطی که به گره i متصل به گره j می پیوندد منطبق است.

همان حرکات بی نهایت کوچک، فریم ورک های بسیارکوچک صلب بیرینگ را در مجموعه اعداد حقیقی با d بعد (d≥2) مشخص می‌کند؛ اندازه گیری بیرینگ بین عوامل i و j با زاویه بین محور x سیستم مختصات محلی گره i و پاره خطی که به گره i متصل به گره j می پیوندد منطبق است. در منابع، برخی از تمایزها معمولاً بین حالت دو بعدی و ابعاد بالاتر انجام می شود، اگرچه در رفرنس [13] یک پایان نامه جامع برای صلبیت یاتاقان ارائه شده است. چندین نتیجه نظری نیز در [13] ارائه شده است، با این حال سهم اصلی شرط لازم و کافی برای تضمین این است که یک فریم ورک معین  با صلبیت بی‎‌نهایت در R^d با d بزرگتر مساوی 2 است. این مورد مربوط به رتبه و مقادیر ویژه یک ماتریس خاص است که قیدهای درگیر را خلاصه می کند.

در رفرنس های [11] و [12]، تئوری صلبیت یاتاقان برای سیستم‌های تعبیه‌شده در SE2 مورد مطالعه قرار گرفته است، به عنوان مثال، چارچوب‌هایی که گراف زیربنایی هدایت می‌شود و یاتاقان‌ها در فریم ورک لوکال هر عامل فریم ورک به‌عنوان یک نقطه SE2 با موقعیت و گرایش خاص خود در صفحه برای مدلسازی در نظر گرفته شده است .

به دلیل ماهیت چندظرفیتی SE2، حرکات بینهایت کوچک حفظ کننده یاتاقان برای یک فریم ورک معین از حرکات در R² با حرکات S1 (چند ظرفیتی یکبعدی روی دایره واحد) تشکیل شده است. بناین نتایج حاصل منجر به انتقالات جسم صلب و مقیاس‌بندی یکنواخت کل مجموعه موقعیت‌ها می‌شوند، اگرچه چرخش‌های هماهنگ همه عوامل حول محور بدنه خود با سرعت زاویه‌ای یکسان، همراه با چرخش بدنه صلب کل فریم ورک در R2 همگام سازی می شوند.

انگیزه اصلی مقاله بیرینگ فعلی به دلیل انجام فرآیند در فضای SE3 است که در واقع به نوعی نوآوری در زمینه صلبیت بیرینگ محسوب می‌شود.

در SE(2)، ویژگی های اساسی چنین تئوری مربوط به اندازه گیری های بیرینگ است که به فریم ورک لوکال هر عامل ارجاع داده می شود (یک نقطه SE(3) موقعیت و جهت خاص خود را در فضای سه بعدی دارد)، این مورد موئید استفاده از گراف جهت‌دار برای نشان دادن اثرمتقابل بین عامل‌هاست. با این وجود، گسترش از فضای دوبعدی ویژه اقلیدسی به فضای سه بعدی بی اهمیت نیست. چالش اصلی به بازنمایی نگرش عوامل می پردازد: در واقع، در حالی که در SE(2) یک زاویه واحد برای تعیین جهت ربات در صفحه کافی است، در فضای سه بعدی باید سه درجه آزادی شامل انواع مختلف و پیچیده تری از منیفولدها مدیریت شود. از این نظر، اگرچه حرکات بینهایت کوچک همچنان دارای انتقالات، مقیاس بندی یکنواخت و چرخش های هماهنگ هستند، اما در متن سیستم جدید با ابعاد بالاتر از نو تعریف شده اند. علاوه بر این، ثابت شده است که آنها فضای خالی ماتریس صلبیت SE(3) نامیده می‌شوند و به طور مشابه مرجع [11]، یک فریم ورک بی‌نهایت صلب در SE (3) است اگر و فقط اگر اندازه فضای تهی این ماتریس برابر با هفت باشد.

مقاله بصورت زیر مرتب شده است. نماد استفاده شده در Sec.II به تصویر کشیده شده است و بررسی مختصری از تئوری صلبیت یاتاقان در R3 در Sec.III ارائه شده است. Sec.IV به توسعه تئوری صلبیت برای SE(3) اختصاص داده شده است، که به وضوح ویژگی های حرکات بی نهایت کوچک مجاز را نشان می دهد، در حالی که چند نمونه در Sec.V آورده شده است. در نهایت، اظهارات پایانی و جهت گیری های تحقیقاتی آینده در بخش ششم مورد بحث قرار می گیرد.

مقدمات و یادداشت

در این مقاله بیرینگ، SE(3)=R³×SO(3) گروه اقلیدسی خاص سه بعدی را نشان می‌دهد که انتقالات جسم صلب در فضای سه بعدی را بیان می‌کند. مخصوصا، SO(3) به گروه دوران سه بعدی بازمی‌گردد، همچنان که منیفولد دوبعدی بر کره واحد در R³ با S² نشان داده شده است. دقت شود که SO(3) با S² هم‌شکل نیست در حالیکه در فضای دوبعدی تثبیت کننده SO(2) ≃ S¹ است.

حالت استاندارد اقلیدسی یک بردار v ∈ R³ با ||v|| نشان داده می‌شود به طوریکه

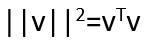
ضرب خارجی بین بردارهای v, u ∈ R³  به صورت v×u = S(v) محاسبه می شود. u، (هنگامی که (.)S نقشه ای است که هر بردار را در R³ به ماتریس انحرافی متقارن مربوطه نظیر به جبر مخالف متعامد ویژه مرتبط می کند) ، so(3) است.

یک گراف جهت‌دار G = (V ,E ) با یک ست راس V و لبه E ⊆ V ×V مشخص می‌شود، به طوریکه |V | = n و |E | = m. گراف با لبه‌های جهت‌دار ممکن یعنی گراف جهت‌دار کامل با m= n(n-1) با k_n نشان داده می‌شود. ارتباط بین ست های V و E با ماتریس برخورد E ∈ R^n×m تعریف می‌شود، به عبارت دیگر ماتریس {0±1} به طوری که:

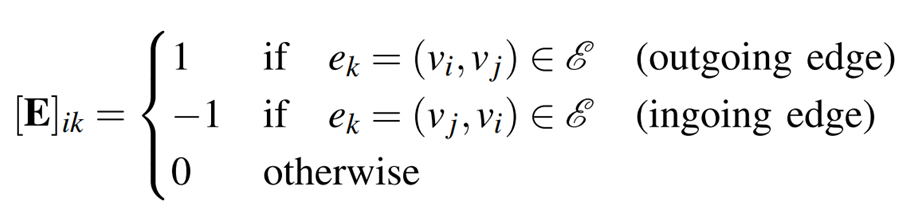
به طور مشابه، E_out ∈ R^n×m ماتریس {0,1} به نحوی طراحی می‌شود که:

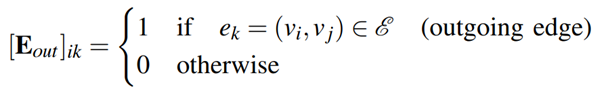
عبارت Ē= E ⊗ I₃ ∈ R^3n×3m و Ē_out = E_out ⊗ I₃ ∈ R^3n×3m نیز معرفی می‌شود.

نهایتا، با توجه به یک ماتریس عمومی A ∈ R^p×q فضای خالی آن با N (A) و ستون (رتبه) آن با rk(A) نمایش داده می‌شود، به طوریکه diag({Ai}) ∈ R^rp×rq به الحاق مورب بلوک تمام ماتریس های {A_i ∈ R^p×q , i = 1,…,r} اشاره دارد.

(مقاله صلبیت بیرینگ)

III. تئوری صلبیت بیرینگ در R³

برخی از مفاهیم اساسی صلبیت بیرینگ در اینجا به اختصار بررسی می‌شوند و بر فریم ورک‌های فیکس شده در R3 تمرکز می‌کنند. پایان نامه جامع تری در مرجع [13] گزارش شده است.

فریم ورکی در R³، نشان داده شه با (G,p)، ، یک جفت متشکل از یک گراف غیر جهت دار G = (V ,E ) و یک ساختار p برابر با:

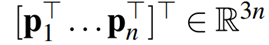
است به طوریکه هر راس v_i ∈ V در گراف با نقطه pi ∈ R³ در ارتباط است. به عبارت دیگر، مجموعه‌ای از n عامل است که می‌تواند بر اساس مجموعه لبه E تعامل داشته باشد، هر یک از آنها با موقعیت خاص p_i در فضای سه‌بعدی تعامل دارند. در نتیجه، برای هر جفت (vi , v j) ∈ E بردار یکه

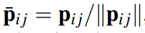
به طوریکه p_{i j} = p_j – p_i، نشان دهنده تحمل بیرینگ نسبی بین v_iو v_j بیان شده با در نظر گرفتن برخی چارچوب‌های مرجع رایج است.

هدف تئوری صلبیت بیرینگ در R³ تعیین این است که چه زمانی یک فریم ورک را می توان به طور منحصر به فرد تا یک انتقال و مقیاس بندی یکنواخت (تحولات حفظ یاتاقان) توسط مجموعه بیرینگ‌های مجاور شناسایی کرد.

به منظور روبرو شدن با این موضوع، تعریف عملگر پروژکتور متعامد P : R3 → R^3×3 سودمند است که از نظر هندسی هر بردار غیر صفر v ∈ R³ را بر روی مکمل متعامد خود نمایش می دهد. این مورد صریحا برقرار کننده رابطه زیر است.

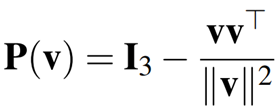
ماتریس طرح متعامد P(v) متقارن، غیر توانمند و مثبت نیمه معین است و فضای تهی آن با فضای تولید شده توسط بردار v، منطبق است (مطابق زیر).

N (P(v)) = span{v}

عملگر طرح متعامد روشی مناسب برای توصیف بردارهای موازی در R³ فراهم می‌کند که در آن مفهوم صلبیت یاتاقان به حفظ موازی برای بخش خط بین هر جفت گره از یک فریم ورک متکی است. در واقع می‌توان گفت دو فریم ورک (G,p) و (‘G,p) بیرینگ برابر هستند اگر P(p_i − p_j) · (p‘_i – p’_j ) = 0 برای هر

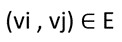
برقرار باشد؛ همچنین بیرینگ متجانس هستند اگر P(p_i−p_j)·(p’_i−p’_j ) = 0 برای هر vi , vj ∈ V برقرار باشد. از این رو، دو فریم ورک متجانس همیشه با یک دنباله محدود مناسب از انتقالات و مقیاس بندی بدنه صلب مرتبط هستند.

مقاله صلبیت بیرینگ، تعریف1: یک فریم ورک (G,p) یک بیرینگ صلب است اگر ε > 0 وجود داشته باشد به طوریکه هر فریم ورک (‘G,p) بیرینگ برابر با (G,P) باشد و رابطه

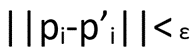
برای هر v_i ∈ V را رعایت می‌کند.

تعریف2: (صلبیت یاتاقان سرتاسری [مرجع 13، تعریف 4]). یک فریم ورک (G,p) به طور سرتاسری صلب است اگر همه فریم ورک‌های معادل (G,p) با (G,p) همخوانی داشته باشند.

همه بیرنگ‌ها در یک فریم‌ورک داده شده توسط عملگر صلبیت بیرینگ:

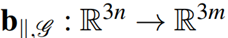
قابل خلاصه‌سازی هستند. این معادله ساختار p درون بردار بیرینگ انباشته را در قالب نقشه درمی‌آورد، یعنی:

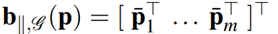
که در آن p̄_kبه اندازه‌گیری‌های k ام لبه برمی‌گردد. ژاکوبین تابع یاتاقان،

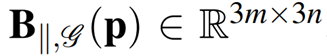
با توجه به تغییر δp ساختار p، اگر

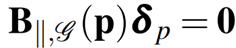
، آنگاه δp یک حرکت بیرینگ بینهایت کوچک از (G,p) نامیده می‌شود. علاوه‌بر این اگر یک حرکت بینهایت کوچک با تبدیل حفظ کننده بیرینگ مطابقت داشته باشد، عموما یک انتقال یا مقیاس‌بندی کل فریم ورک، به عنوان مقدار ناچیز در نظر گرفته می‌شود.

تعریف 3: (صلبیت بیرینگ بی‌نهایت کوچک، رفرنس 13 تعریف 5):

در صورتی که هر حرکت بی نهایت کوچک ممکن بی اهمیت باشد، یک فریم ورک (G,p) به طور بی نهایت صلب است.

ویژگی‌های صلبیت بیرینگ‌های بی‌نهایت کوچک یک فریم ورک به فضای تهی و رتبه ماتریس صلبیت نظیر مرتبط است.

قضیه 1: (شرایط صلبیت بیینگ بینهایت کوچک، رفرنس 13 قضیه4):

برای فریم ورک (G,p) در R³، عبارات زیر برقرارند:

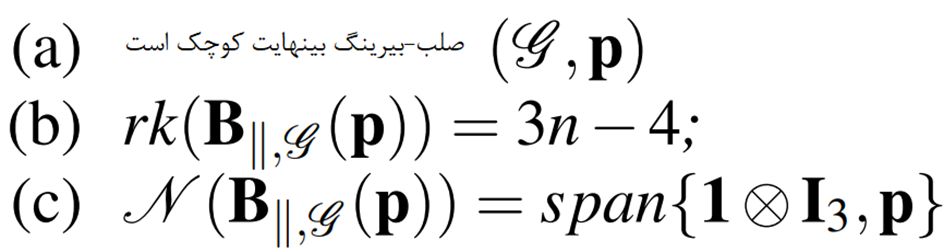
علاوه بر این، قابل اثبات است که صلبیت بیرینگ بینهایت کوچک، یک خاصیت قوی‌تر از هر دو مورد بیرینگ و بیرینگ سرتاسری است که در طرف دیگر معادله قرار می‌گیرند.

قضیه2: (خواص صلبیت). برای یک فریم ورک (G,p) در R³، مفاهیم زیر معتبرند:

صلبیت سرتاسری بیرینگ ⇔ صلبیت بیرینگ

صلبیت سرتاسری بیرینگ ⇒ صلبیت بینهایت کوچک بیرینگ

صلبیت بیرینگ ⇒ صلبیت بینهایت کوچک بیرینگ

برخی از ویژگی های اصلی صلبیت یاتاقان در R3 را می توان از جدول I استخراج نمود که یک نمای کلی در مورد طبقه بندی مورد استفاده در ادبیات صلبیت با توجه به حوزه گره ها و اندازه گیری ها ارائه می دهد.

مقاله صلبیت بیرینگ

IV. (تئوری صلبیت در SE(3))

مفاهیم معرفی شده در بخش قبل برای گسترش تئوری صلبیت برای فریم‌ورک‌هایی که در گروه اقلیدسی ویژه سه بعدی SE (3) تعبیه شده اند، مورد نیاز است. در اینجا، هر عامل با یک موقعیت و یک جهت در فضای سه بعدی مشخص می شود و فرض می شود که با همسایگان خود مطابق با یک گراف جهت دار خاص تعامل دارد.

تعریف4: (فریم ورک SE(3)). یک فریم‌ورک SE(3) در واقع سه‌گانه (G,p,a) است، که در آن G=(V,E) یک گراف جهت دار است، p : V → R³ تابعی است که هر گره را به عنوان نقطه‌ای در R³ به نقشه درمی‌آورد و a : V → SO(3) تابعی است که هر گره را با یک المان در SO(3) (جهت) همراه می‌سازد.

در منابع، فرمالیسم‌های مختلفی معروفی برای نمایش جهت عاملی که قادر به حرکت در فضای سه‌بعدی است، وجود دارد، به‌عنوان مثال، زوایای اویلر، کواترنیون‌ها، بازنمایی محور-زاویه. در این کار، جهت گیری عامل ها از طریق ماتریس های چرخشی، که به گروه متعامد ویژه SO(3) تعلق دارند، بیان می شود. این گروه شامل تمام ماتریس های متعامد 3×3 با تعیین واحد می باشد. بنابراین در ادامه راستای هر عامل i باید به عنوان یک ماتریس دوران R_i ∈ R^3×3 و det(R_i) = +1 تعبیر شود.

از این پس برای سهولت نمادگذاری، موقعیت و جهت گره v_i ∈ V توسط:

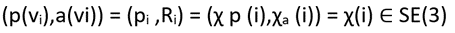
نمایش داده می‌شود که در آن:

p(V ) = χ_p(V ) ∈ R³ⁿ

و

 a(V ) = χ_a(V)∈ SO(3)ⁿ

به ترتیب موقیعت و جهت اجزا ساختار فریم ورک کامل را نشان می‌دهد.

مشابه مورد SE(2) (برای جزئیات بیشتر به رفرنس‌های [11] و [12] مراجعه کنید)، پسوند به SE(3) صریحا فریم‌ورک‌هایی را کنترل می کند که در آن نمودار زیرین هدایت می شود و یاتاقان ها در قاب بدنه لوکال هر عامل بیان می شوند (نقطه SE(3)).

این مفروضات با سناریوهای چند عامله واقعی توجیه می شوند که در آن یک ربات می تواند یاتاقان های نسبی را بین خود و سایر ربات ها از طریق حسگرهای متصل به قاب بدنه اش جمع آوری کند، مانند ربات هایی که به صورت سه بعدی با دوربین های داخل هواپیما پرواز می‌کنند.

در این مکان، عامل i به یاتاقان عامل j دسترسی پیدا می‌کند اگر و تنها اگر یال جهت‌دار (vi، vj) متعلق به نمودار G باشد. علاوه بر این، بیرینگ نسبی bij ∈ S2 از سیستم مختصات بدن عامل i اندازه گیری می شود، اما می توان آن را بر حسب موقعیت ها و راستاهای نسبی دو نقطه با توجه به چارچوب کلی بیان نمود. این مورد را بطه زیر برقرار می‌سازد:

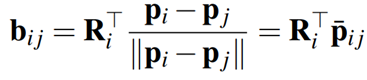
که در آن ماتریس R^T_i ماتریس دوران و معرف جهت چارچوب کلی با توجه به بدنه چارچوب عامل ، و p̄_ij یک نماد کوتاه برای بردار موقعیت نسبی نرمال شده از i تا j است.

تئوری صلبیت بیرینگ در SE (3) به دنبال ارزیابی خواص صلبیت یک فریم ورک معین (G,p,a) است که بر حفظ اندازه‌گیری‌های بیرینگ استوار است. به عبارت دیگر، هدف اصلی شناسایی حرکات مجاز است که کل سیستم ها را از نظر یاتاقان‌های بین عاملی تغییر نمی دهند.